题目内容
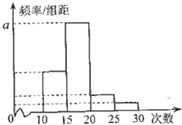 对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由频数、频率和样本容量的关系,可求M=40,故m值可求,进而求p=
;
(2)由(1)可得,参加社区服务的次数不少于20次的学生为5人,从中任选2人,共有10种不同的结果,写出这10个基本事件,事件“至多一人参加社区服务次数在区间[20,25)内”的对立事件为“选出的2人都在区间[20,25)内”,数出结果数,代入古典概型的概率计算公式,利用对立事件概率公式来求.
| 3 |
| 40 |
(2)由(1)可得,参加社区服务的次数不少于20次的学生为5人,从中任选2人,共有10种不同的结果,写出这10个基本事件,事件“至多一人参加社区服务次数在区间[20,25)内”的对立事件为“选出的2人都在区间[20,25)内”,数出结果数,代入古典概型的概率计算公式,利用对立事件概率公式来求.
解答:
解:(1)由分组[10,15)内的频数是10,频率是0.25知,
=0.25,所以M=40.2分
因为频数之和为40,所以10+25+m+2=40,m=3.p=
=
. 4分
因为a是对应分组[15,20)的频率与组距的商,所以a=
=0.125 6分
(2)这个样本参加社区服务的次数不少于20次的学生共有3+2=5人,
设在区间[20,25)内的人为{a,b,c},在区间[25,30)内的人为{e,d}.
则任选2人共有(a,b),(a,c),(a,e),(a,d),(b,c),(b,e),(b,d),(c,e),(c,d),(e,d),10种情况,8分
而两人都在[20,25)内共有(a,b),(a,c),(a,e),3种,10分
至多一人参加社区服务次数在区间[20,25)内的概率p=1-
=
. 12分
| 10 |
| M |
因为频数之和为40,所以10+25+m+2=40,m=3.p=
| 3 |
| M |
| 3 |
| 40 |
因为a是对应分组[15,20)的频率与组距的商,所以a=
| 25 |
| 40×5 |
(2)这个样本参加社区服务的次数不少于20次的学生共有3+2=5人,
设在区间[20,25)内的人为{a,b,c},在区间[25,30)内的人为{e,d}.
则任选2人共有(a,b),(a,c),(a,e),(a,d),(b,c),(b,e),(b,d),(c,e),(c,d),(e,d),10种情况,8分
而两人都在[20,25)内共有(a,b),(a,c),(a,e),3种,10分
至多一人参加社区服务次数在区间[20,25)内的概率p=1-
| 3 |
| 10 |
| 7 |
| 10 |
点评:本题考查古典概型以及频率分布直方图的应用,考查计算能力.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
表面积为4
的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=3sin(2x+
)图象可以看作把函数y=3sin2x的图象作下列移动而得到( )
| 6 |
| 5 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移y=sin(2x+
|
如图所示正方体AC1,下面结论错误的是( )
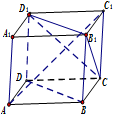

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AD与CB1角为60° |
下列各组函数f(x)与g(x)的图象相同的是( )
A、f(x)=x,g(x)=(
| |||||
| B、f(x)=x2,g(x)=(x+1)2 | |||||
C、f(x)=|x|,g(c)=
| |||||
| D、f(x)=1,g(x)=x0 |
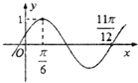 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|