题目内容
7．等差数列{an}的前n项和为Sn，S5=-5，S9=-45，则a4的值为（ ）| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
分析 由题意和等差数列的性质可得a3和a5，再由等差数列的性质可得a4=$\frac{{a}_{3}+{a}_{5}}{2}$，代值计算可得．
解答 解：由题意和等差数列的性质可得S5=$\frac{5（{a}_{1}+{a}_{5}）}{2}$=$\frac{5×2{a}_{3}}{2}$=5a3=-5，
解得a3=-1，同理可得S9=9a5=-45，解得a5=-5，
再由等差数列的性质可得a4=$\frac{{a}_{3}+{a}_{5}}{2}$=-3
故选：C
点评 本题考查等差数列的求和公式和等差数列的性质，属基础题．
练习册系列答案
相关题目
如图，已知△OCB中，B、C关于点A对称，D是将OB分成2：1的一个内分点，DC和OA交于点E，设$\overrightarrow{OA}=\overrightarrow a，\overrightarrow{OB}=\overrightarrow b$．
2．
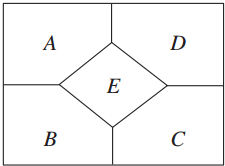如图所示的五个区域中，现有四种颜色可供选择．要求每一个区域只涂一种颜色，相邻区域所涂颜色不同，则不同的涂色方法种数为（ ）
如图所示的五个区域中，现有四种颜色可供选择．要求每一个区域只涂一种颜色，相邻区域所涂颜色不同，则不同的涂色方法种数为（ ）| A． | 24种 | B． | 48种 | C． | 72种 | D． | 96种 |
12．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张．从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（ ）
| A． | 484 | B． | 472 | C． | 252 | D． | 232 |
16．已知离心率为$\frac{1}{2}$的椭圆的左右焦点分别为F1，F2，椭圆上一点P满足：|PF1|=2|PF2|，则cos∠PF1F2=（ ）
| A． | $\frac{11}{16}$ | B． | $\frac{7}{8}$ | C． | -$\frac{1}{4}$ | D． | 不确定 |