题目内容
5.在△ABC中,∠A=45°,a=$\sqrt{5}$,b=4,满足条件的△ABC( )| A. | 不存在 | B. | 有一个 | C. | 有两个 | D. | 有无数多个 |
分析 由题意比较bsinA和a的大小可得.
解答 解:由题意可得bsinA=4×sin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
比较可得a=$\sqrt{5}$<2$\sqrt{2}$,
∴三角形无解.
故选:A.
点评 本题考查三角形解得个数的判断,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设x=50.6,y=0.65,z=log0.65,则x,y,z的大小关系为( )
| A. | y<z<x | B. | y<x<z | C. | z<x<y | D. | z<y<x |
13.已知集合A={log2a,3},B={a,b},若A∩B={0},则A∪B=( )
| A. | {0,3} | B. | {0,1,3} | C. | {0,2,3} | D. | {0,1,2,3} |
17.不等式$\frac{3-4x}{1-2x}$≤1的解集为( )
| A. | [1,+∞) | B. | ($\frac{1}{2}$,1) | C. | [$\frac{1}{2}$,1] | D. | ($\frac{1}{2}$,1] |
15.函数y=cos(x+$\frac{π}{6}$),x∈[0,$\frac{π}{2}$].的值域是( )
| A. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{3}}{2}$,1] | D. | [$\frac{1}{2}$,1] |
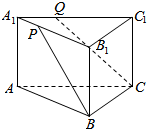 如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.
如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.