题目内容
7.四棱锥S-ABCD的底面是边长为2的正方形,点S,A,B,C,D均在半径为$\sqrt{3}$的同一半球面上,则当四棱锥S-ABCD的体积最大时,底面ABCD的中心与顶点S之间的距离为( )| A. | 2-$\sqrt{3}$ | B. | 2 | C. | $\sqrt{4+\sqrt{6}}$ | D. | $\sqrt{3}$+1 |
分析 画出图形,判断四棱锥体积最大时S的位置,然后求解底面ABCD的中心与顶点S之间的距离即可.
解答 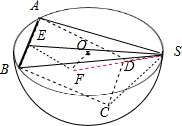 解:四棱锥S-ABCD的底面是边长为2的正方形,点S,A,B,C,D均在半径为$\sqrt{3}$的同一半球面上,则当四棱锥S-ABCD的体积最大时,顶点S与球心的连线恰好底面ABCD的一边的中点,如图:
解:四棱锥S-ABCD的底面是边长为2的正方形,点S,A,B,C,D均在半径为$\sqrt{3}$的同一半球面上,则当四棱锥S-ABCD的体积最大时,顶点S与球心的连线恰好底面ABCD的一边的中点,如图:
此时球心O到底面中心F的距离为:OF=${\sqrt{{(\sqrt{3})}^{2}-(\sqrt{2})^{2}}}^{\;}$=1.即EF=OF=1,
∠SEF=45°,
SE=$\sqrt{3}+\sqrt{2}$,SF=$\sqrt{{EF}^{2}+{ES}^{2}-2EF•EScos45°}$=$\sqrt{4+\sqrt{6}}$
所求距离为:$\sqrt{4+\sqrt{6}}$.
故选:C.
点评 本题考查球的内接体,几何体的高的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目