题目内容
已知椭圆 和椭圆
和椭圆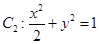 的离心率相同,且点
的离心率相同,且点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)设 为椭圆
为椭圆 上一点,过点
上一点,过点 作直线交椭圆
作直线交椭圆 于
于 、
、 两点,且
两点,且 恰为弦
恰为弦 的中点。求证:无论点
的中点。求证:无论点 怎样变化,
怎样变化, 的面积为常数,并求出此常数.
的面积为常数,并求出此常数.
 和椭圆
和椭圆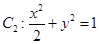 的离心率相同,且点
的离心率相同,且点 在椭圆
在椭圆 上.
上.(1)求椭圆
 的方程;
的方程;(2)设
 为椭圆
为椭圆 上一点,过点
上一点,过点 作直线交椭圆
作直线交椭圆 于
于 、
、 两点,且
两点,且 恰为弦
恰为弦 的中点。求证:无论点
的中点。求证:无论点 怎样变化,
怎样变化, 的面积为常数,并求出此常数.
的面积为常数,并求出此常数.(1)椭圆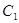 的方程为
的方程为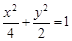 ;(2)
;(2)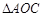 的面积为常数
的面积为常数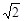 .
.
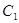 的方程为
的方程为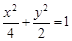 ;(2)
;(2)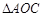 的面积为常数
的面积为常数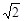 .
.试题分析:(1)由题知,
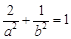 且
且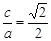 ,
,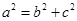 解这个方程组求得
解这个方程组求得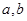 即可得椭圆
即可得椭圆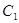 的方程;(2)涉及直线与曲线的关系的问题,多是将直线方程与曲线方程联立再用韦达定理解决.此题中有两个椭圆,将哪个椭圆的方程与直线方程联立?此题意即直线与
的方程;(2)涉及直线与曲线的关系的问题,多是将直线方程与曲线方程联立再用韦达定理解决.此题中有两个椭圆,将哪个椭圆的方程与直线方程联立?此题意即直线与 的交点的中点在
的交点的中点在 上,故应将直线方程与
上,故应将直线方程与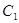 的方程联立由韦达定理得中点坐标,再将中点坐标代入
的方程联立由韦达定理得中点坐标,再将中点坐标代入 的方程.然后求出三角形OAB的面积的表达式,再利用前面所得关系式化为一常数即可.
的方程.然后求出三角形OAB的面积的表达式,再利用前面所得关系式化为一常数即可. 试题解析:(1)由题知,
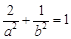 且
且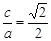 即
即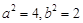 ,
, 椭圆
椭圆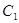 的方程为
的方程为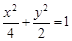 ; 4分
; 4分(2)当直线
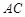 的斜率不存在时,必有
的斜率不存在时,必有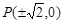 ,此时
,此时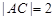 ,
,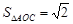 5分
5分当直线
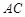 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为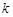 、点
、点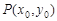 ,则
,则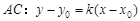
与椭圆
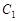 联立,得
联立,得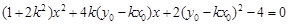 ,设
,设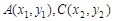 ,
,则
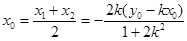 即
即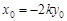 8分
8分又
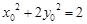
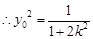 9分
9分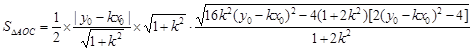
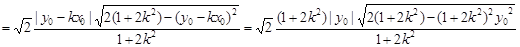
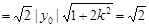
综上,无论
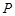 怎样变化,
怎样变化,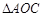 的面积为常数
的面积为常数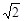 . 12分
. 12分
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 ,过
,过 的直线与曲线
的直线与曲线 ,过
,过 的直线与曲线
的直线与曲线 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 ,设点
,设点 (
( ).
). ,并求
,并求 与
与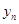 的关系式(
的关系式( (
( ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由; ,数列
,数列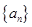 的前
的前 项和为
项和为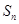 ,试比较
,试比较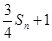 与
与 的大小,并证明你的结论.
的大小,并证明你的结论. 的离心率为
的离心率为 ,过左焦点
,过左焦点 且斜率为
且斜率为 的直线交椭圆E于A,B两点,线段AB的中点为M,直线
的直线交椭圆E于A,B两点,线段AB的中点为M,直线 :
: 交椭圆E于C,D两点.
交椭圆E于C,D两点.
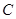 的两个焦点为
的两个焦点为 ,
, ,一个顶点式
,一个顶点式 ,则
,则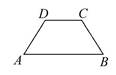
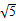 ,+∞)
,+∞)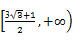
 =1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足|
=1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足| |=3|
|=3| |,则此双曲线的渐近线方程为________.
|,则此双曲线的渐近线方程为________.



 的中心在坐标原点,对称轴为坐标轴,焦点在
的中心在坐标原点,对称轴为坐标轴,焦点在 轴上,有一个顶点为
轴上,有一个顶点为 ,
, .
. 作直线
作直线 与椭圆
与椭圆 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围. =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1. +
+ 为定值,并求出这个定值.
为定值,并求出这个定值.