题目内容
【题目】已知函数f(x)![]() ,k≠0,k∈R.
,k≠0,k∈R.
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)已知f(x)在(﹣∞,0]上单调递减,求实数k的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意,由函数的解析式分析可得![]() 的表达式,讨论
的表达式,讨论![]() 的范围,分析
的范围,分析![]() 与
与![]() 的关系,即可得结论;
的关系,即可得结论;
(2)设![]() ,分析可得
,分析可得![]() 的范围,则
的范围,则![]() 对
对![]() 的范围进行分情况讨论,讨论函数
的范围进行分情况讨论,讨论函数![]() 的单调性,求出
的单调性,求出![]() 的范围,综合即可得答案.
的范围,综合即可得答案.
(1)根据题意,函数f(x)![]() ,其定义域为R,
,其定义域为R,
f(-x)![]() =
=![]() ,当k=1时,有f(x)=f(﹣x),函数f(x)为偶函数,
,当k=1时,有f(x)=f(﹣x),函数f(x)为偶函数,
当k≠1时,f(x)≠f(﹣x)且f(﹣x)≠﹣f(x),函数f(x)为非奇非偶函数;
(2)设t=2x,x∈(﹣∞,0],则有0<t≤1,则y=![]() ,
,
当k<0时,函数f(x)在R上递减,符合题意;
当k>0时,t∈(0,![]() )上时,函数y=
)上时,函数y=![]() 递减,t∈(
递减,t∈(![]() ,+∞)上时,函数y=
,+∞)上时,函数y=![]() 递增,若已知f(x)在(﹣∞,0]上单调递减,必有
递增,若已知f(x)在(﹣∞,0]上单调递减,必有![]() ≥1,解可得k≥1,
≥1,解可得k≥1,
综合可得:t的取值范围是(﹣∞,0)∪[1,+∞).

练习册系列答案
相关题目
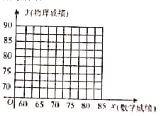
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中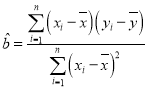 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.