题目内容
在直三棱柱ABC—A1B1C1中,AB=AC=AA1=6,BC=4,D是BC的中点,F是C1C上一点,且CF=4。
(1)求证:B1F⊥平面ADF;
(2)求三棱锥D—AB1F的体积;
(3)试在AA1上找一点E,使得BE//平面ADF。
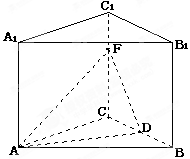
(1)求证:B1F⊥平面ADF;
(2)求三棱锥D—AB1F的体积;
(3)试在AA1上找一点E,使得BE//平面ADF。

(1)∵AB=AC,D为BC的中点
∴AD⊥BC,又直三棱柱中:BB1⊥底面ABC,AD 底面ABC。∴AD⊥BB1
底面ABC。∴AD⊥BB1
∴AD⊥平面BCC1B1,∵B1F 平面BCC1B1,∴AD⊥B1F,
平面BCC1B1,∴AD⊥B1F,
在矩形BCC1B1中:C1F=CD=2,CF=C1B1=1,
∴ ,∴
,∴ ,即B1F⊥FD,
,即B1F⊥FD,
∵ ∴B1F⊥平面AFD………………..4分
∴B1F⊥平面AFD………………..4分
(2)∵AD⊥平面BCC1B1,
∴ …….8分
…….8分

∴AD⊥BC,又直三棱柱中:BB1⊥底面ABC,AD
 底面ABC。∴AD⊥BB1
底面ABC。∴AD⊥BB1∴AD⊥平面BCC1B1,∵B1F
 平面BCC1B1,∴AD⊥B1F,
平面BCC1B1,∴AD⊥B1F,在矩形BCC1B1中:C1F=CD=2,CF=C1B1=1,
∴
 ,∴
,∴ ,即B1F⊥FD,
,即B1F⊥FD,∵
 ∴B1F⊥平面AFD………………..4分
∴B1F⊥平面AFD………………..4分(2)∵AD⊥平面BCC1B1,
∴
 …….8分
…….8分
略

练习册系列答案
相关题目
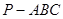 中,
中,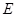 为
为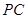 的中点,则
的中点,则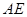 与平面
与平面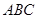 所成的角的正弦值为( )
所成的角的正弦值为( )



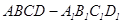 中,
中,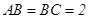 ,
,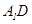 与
与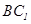
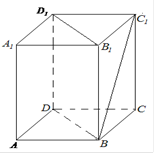
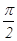 ,则
,则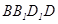 所成角的正弦值为( )
所成角的正弦值为( )



 的等腰直角三角形
的等腰直角三角形 与正三角形
与正三角形 所在平面互相垂直,
所在平面互相垂直, 是线段
是线段 的中点,则
的中点,则 与
与 所成角的大小为 .
所成角的大小为 .
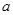 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,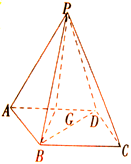
 中,
中, ,
, ,则
,则 与平面
与平面 所成角的正弦值为 .
所成角的正弦值为 .
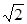 BB1,则AB1与C1B所成的角的大小为( )
BB1,则AB1与C1B所成的角的大小为( )


