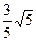题目内容
在直角坐标系xOy中，直线x－2y＋4＝0与椭圆＋＝1交于A，B两点，F是椭圆的左焦点．求以O，F，A，B为顶点的四边形的面积．
(72＋7)．
：取方程组代入得，25y2－64y＋28＝0．
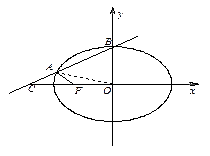
此方程的解为y＝2，y＝．即得B(0，2)，A(－，)，
又左焦点F1(－，0)．连OA把四边形AFOB分成两个三角形．
得，S＝×2×＋××＝(72＋7)．
也可以这样计算面积：直线与x轴交于点C(－4，0)．所求面积＝×4×2－×(4－)×＝(72＋7)．也可以这样计算面积：所求面积＝(0×2－0×0＋0×－(－)×2＋(－)×0－(－)×＋(－)×0－0×0)＝(＋)＝(72＋7)．
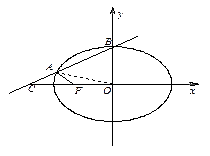
此方程的解为y＝2，y＝．即得B(0，2)，A(－，)，
又左焦点F1(－，0)．连OA把四边形AFOB分成两个三角形．
得，S＝×2×＋××＝(72＋7)．
也可以这样计算面积：直线与x轴交于点C(－4，0)．所求面积＝×4×2－×(4－)×＝(72＋7)．也可以这样计算面积：所求面积＝(0×2－0×0＋0×－(－)×2＋(－)×0－(－)×＋(－)×0－0×0)＝(＋)＝(72＋7)．
练习册系列答案
相关题目
与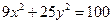
的焦距相等，则
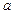的值为（ ）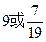
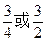
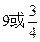
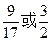
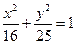表示的曲线是（ ）
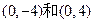的距离之和等于
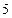的点的轨迹
的点的轨迹
的距离之和等于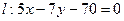
上的点
作椭圆
的切线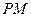
、
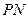，切点分别为
、
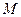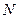，联结
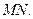（1）当点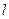
上运动时，证明：直线
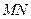恒过定点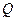
；
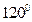，则此椭圆的离心率
为（ ）
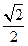
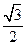
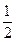
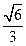
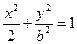的焦点为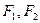
,两条准线与x轴的交点分别为M、N，若
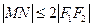，则该椭圆离心率取得最小值时的椭圆方程为 ( )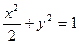
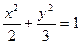
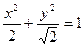
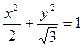
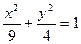，椭圆左焦点为
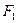，O为坐标原点，A是椭圆上一点，点M在线段
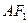上且，
，则点A的横坐标为（ ）
