题目内容
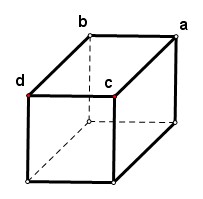
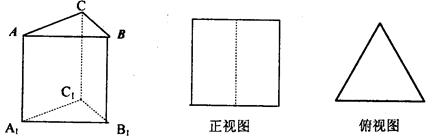
长方体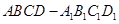 的各顶点都在半径为1的球面上,其中
的各顶点都在半径为1的球面上,其中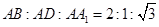 ,则两
,则两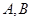 点的球面距离为( )
点的球面距离为( )
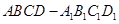 的各顶点都在半径为1的球面上,其中
的各顶点都在半径为1的球面上,其中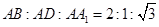 ,则两
,则两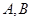 点的球面距离为( )
点的球面距离为( )A.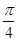 | B.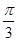 | C.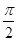 | D.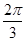 |
C
设出AD,然后通过球的直径求出AD,解出∠AOB,可求A,B两点的球面距离.
解答:解:设AD=a,则AB=2a,AA1=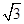 a?球的直径2R=
a?球的直径2R= =2
=2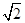 a
a
即R=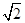 a,在△AOB中,OA=OB=R=
a,在△AOB中,OA=OB=R=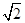 a,AB=2a,
a,AB=2a,
?OA2+OB2=AB2?∠AOB=90°从而A,B点的球面距离为 ?2π=
?2π=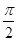
故选C.
解答:解:设AD=a,则AB=2a,AA1=
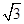 a?球的直径2R=
a?球的直径2R= =2
=2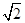 a
a即R=
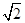 a,在△AOB中,OA=OB=R=
a,在△AOB中,OA=OB=R=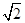 a,AB=2a,
a,AB=2a,?OA2+OB2=AB2?∠AOB=90°从而A,B点的球面距离为
 ?2π=
?2π=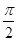
故选C.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
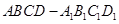 中,
中,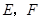 分别为棱
分别为棱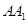 ,
,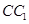 的中点,则在空间中与三条直线
的中点,则在空间中与三条直线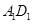 ,
,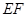 ,
,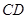 都相交的直线( )
都相交的直线( )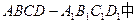 ,
, ,点M是棱
,点M是棱 的中点.
的中点. 直线
直线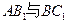 是异面直线;
是异面直线; 所成的角(结果用反三角函数值表示).
所成的角(结果用反三角函数值表示).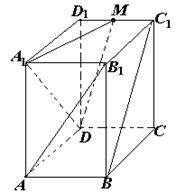

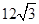
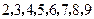 这八个数放在长方体的八个顶点上,使六个面中
这八个数放在长方体的八个顶点上,使六个面中