题目内容
数列{an}的通项an=(-1)n+1•n2,观察以下规律:
a1=1
a1+a2=1-4=-3=-(1+2)
a1+a2+a3=1-4+9=6=1+2+3
…
试写出求数列{an}的前n项和Sn的公式,并用数学归纳法证明.
a1=1
a1+a2=1-4=-3=-(1+2)
a1+a2+a3=1-4+9=6=1+2+3
…
试写出求数列{an}的前n项和Sn的公式,并用数学归纳法证明.
Sn=a1+a2+a3+…+an=(-1)n+1•
证明:(1)当n=1时,Sn=1命题成立;
(2)假设当n=k时命题成立,即Sk=(-1)k+1•
则当n=k+1时,Sk+1=Sk+ak+1=(-1)k+1•
+(-1)k+2•(k+1)2,
=(-1)k+2
•(k+2)
,即命题也成立
综上(1)(2),命题成立.
| n(n+1) |
| 2 |
证明:(1)当n=1时,Sn=1命题成立;
(2)假设当n=k时命题成立,即Sk=(-1)k+1•
| k(k+1) |
| 2 |
则当n=k+1时,Sk+1=Sk+ak+1=(-1)k+1•
| k(k+1) |
| 2 |
=(-1)k+2
| k+1 |
| 2 |
,即命题也成立
综上(1)(2),命题成立.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目

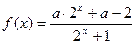 为奇函数.
为奇函数.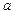 的值;
的值;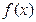 在其定义域上为增函数
在其定义域上为增函数
 (
( 为虚单位),则
为虚单位),则 的模
的模 = 。
= 。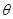 为实数,若复数
为实数,若复数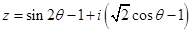 是纯虚数,则
是纯虚数,则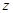 的虚部为( )
的虚部为( )



 求证:
求证: