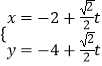题目内容
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0 , 则称x0是f(x)的一个不动点.
(1)若函数f(x)=2x+ ![]() ﹣5,求此函数的不动点;
﹣5,求此函数的不动点;
(2)若二次函数f(x)=ax2﹣x+3在x∈(1,+∞)上有两个不同的不动点,求实数a的取值范围.
【答案】
(1)解:函数f(x)=2x+ ![]() ﹣5,
﹣5,
由f(x)=x,即x+ ![]() ﹣5=0,
﹣5=0,
即为x2﹣5x+4=0,解得x=1和4,
则此函数的不动点为1,4
(2)解:二次函数f(x)=ax2﹣x+3在x∈(1,+∞)上有两个不同的不动点,
即为ax2﹣2x+3=0在x∈(1,+∞)上有两个不等的实根,
当a>0时,△=4﹣12a>0,且a﹣2+3>0, ![]() >0,解得0<a<
>0,解得0<a< ![]() ;
;
当a<0,由于对称轴x= ![]() <0,在x∈(1,+∞)上没有两个不等的实根,不成立.
<0,在x∈(1,+∞)上没有两个不等的实根,不成立.
综上可得,0<a< ![]() .
.
则实数a的取值范围为(0, ![]() )
)
【解析】(1)由定义可得f(x)=x,解方程即可得到所求不动点;(2)由题意可得ax2﹣2x+3=0在x∈(1,+∞)上有两个不等的实根,讨论a>0或a<0和判别式大于0,对称轴介于x=1的右边,x=1的函数值大于0,解不等式即可得到所求范围.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() x+
x+![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?