题目内容
【题目】设函数f（x）的定义域为D，若f（x）满足条件：存在[a，b]D，使f（x）在[a，b]上的值域是[ 
， 
]，则成f（x）为“倍缩函数”，若函数f（x）=log2（2x+t）为“倍缩函数”，则t的范围是（ ）
A.（0， 
）
B.（0，1）
C.（0， 
]
D.（ ，+∞）
【答案】A
【解析】解：∵函数f（x）= 
为“倍缩函数”，
且满足存在[a，b]D，使f（x）在[a，b]上的值域是[ 
， 
]，
∴f（x）在[a，b]上是增函数；
∴ 
，
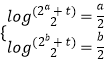即 
，
∴方程 
+t=0有两个不等的实根，且两根都大于0；
∴ 
，
解得：0＜t＜ 
，
∴满足条件t的范围是（0， ），
故答案选：A．
【考点精析】利用函数的值域对题目进行判断即可得到答案，需要熟知求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．
练习册系列答案
相关题目
