题目内容
2.若α、β∈(0,$\frac{π}{2}$),且有sinα-sinβ=-$\frac{2}{3}$,cosα-cosβ=$\frac{2}{3}$,则tan(α-β)的值为( )| A. | $\frac{2\sqrt{14}}{5}$ | B. | -$\frac{2\sqrt{14}}{5}$ | C. | ±$\frac{2\sqrt{14}}{5}$ | D. | ±$\frac{5\sqrt{14}}{28}$ |
分析 吧所给的2个式子平方相加,利用两角和差的余弦公式求得cos(α-β)=$\frac{5}{9}$,再结合0<α<β<$\frac{π}{2}$,利用同角三角函数的基本关系求得 sin(α-β)的值,可得tan(α-β)的值.
解答 解:由α、β∈(0,$\frac{π}{2}$),sinα-sinβ=-$\frac{2}{3}$,cosα-cosβ=$\frac{2}{3}$,可得0<α<β<$\frac{π}{2}$,
且$\left\{\begin{array}{l}{{sin}^{2}α{+sin}^{2}β-2sinαsinβ=\frac{4}{9}}\\{{cos}^{2}α{+cos}^{2}β-2cosαcosβ=\frac{4}{9}}\end{array}\right.$,两式相加求得cos(α-β)=$\frac{5}{9}$,
∴sin(α-β)=-$\sqrt{{1-cos}^{2}(α-β)}$=-$\frac{2\sqrt{14}}{9}$,∴tan(α-β)=$\frac{sin(α-β)}{cos(α-β)}$=-$\frac{2\sqrt{14}}{5}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系、两角和差的余弦公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知点A(-1,-1)和向量$\overrightarrow a$=(2,3),若$\overrightarrow{AB}$=3$\overrightarrow a$,则点B的坐标是(5,8).
13.已知点An(n,an)(n∈N*)都在函数y=ax(a>0,a≠1)的图象上,则a4+a6与2a5的大小关系是( )
| A. | a4+a6>2a5 | B. | a4+a6<2a5 | ||
| C. | a4+a6=2a5 | D. | a4+a6与2a5的大小与a有关 |
10.已知函数f(x)=$\frac{{e}^{x}+m}{{e}^{x}+1}$,若对?a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是[$\frac{1}{2}$,2].
17.如果如图程序执行后输出的结果是11880,那么在程序UNTIL后面的“条件”应为( ) 

| A. | i>9 | B. | i>=9 | C. | i<=9 | D. | i<9 |
7.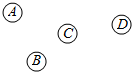 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )| A. | 8种 | B. | 12种 | C. | 16种 | D. | 20种 |
14.若函数f(x)=$\sqrt{3}$cos(2x+α)-sin(2x+α)的图象关于直线x=0对称,则α=( )
| A. | α=kπ-$\frac{π}{3}$(k∈Z) | B. | α=kπ-$\frac{π}{6}$(k∈Z) | C. | α=kπ+$\frac{π}{3}$(k∈Z) | D. | α=kπ+$\frac{π}{6}$(k∈Z) |
11.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第36颗珠子的颜色是 ( )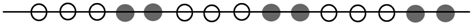
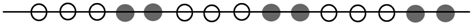
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |