题目内容
直线l：y＝x＋a(a≠0)和曲线C：y＝x3－x2＋1相切，求切点
的坐标及a的值．
的坐标及a的值．
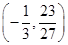，a＝
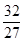.设切点A(x0，y0)，
?
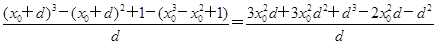＝3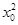
－2x0＋(3x0－1)d＋d2→3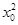－2x0(d→0)．
故曲线上点A处切线斜率为3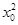－2x0，∴3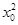－2x0＝1，
∴x0＝1或x0＝－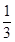
，代入C的方程得
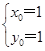或
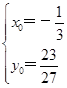代入直线l，
当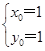时，a＝0(舍去)，当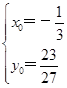时，a＝，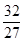
即切点坐标为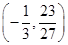，a＝.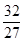
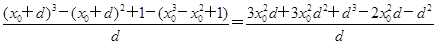?＝3
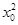－2x0＋(3x0－1)d＋d2→3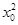－2x0(d→0)．故曲线上点A处切线斜率为3
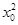－2x0，∴3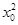－2x0＝1，∴x0＝1或x0＝－
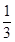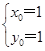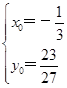，代入C的方程得或代入直线l，当
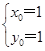时，a＝0(舍去)，当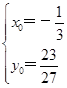时，a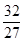＝，即切点坐标为
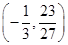，a＝.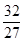
练习册系列答案
相关题目
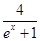上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )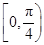
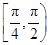
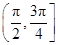
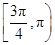
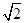
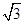
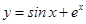的图象上一点（0,1）处的切线的斜率为( )
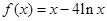，则曲线
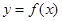在点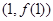
处的切线方程为___________.