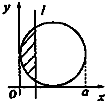题目内容
9．函数f（x）=x3-ax2-bx+a2在x=1处有极值10，则a，b的值为（ ）| A． | $\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$ | D． | 以上都不对 |
分析 利用函数值，函数的导数列出方程求解即可．
解答 解：函数f（x）=x3-ax2-bx+a2，f′（x）=3x2-2ax-b，
函数f（x）=x3-ax2-bx+a2在x=1处有极值10，
可得：$\left\{\begin{array}{l}3-2a-b=0\\ 1-a-b+{a}^{2}=10\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$，
当$\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$时，f′（x）=3x2-6x+3≥0恒成立，x=1不是极值点．
当$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$时，f′（x）=3x2+8x-11，△=196＞0，导函数有两个解，x=1是极值点．满足题意；
故选：B．
点评 本题考查函数的导数的应用，函数的极值的应用，注意验证，否则容易错选A．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
4．在△ABC中，A=60°，若a，b，c成等比数列，则$\frac{bsinB}{c}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
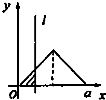
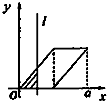
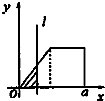
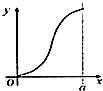如图，有四个平面图形分别是三角形、平行四边形、直角梯形、圆．垂直于x轴的直线l：x=t（0≤t≤a）经过原点O向右平行移动，l在移动过程中扫过平面图形的面积为y（图中阴影部分），若函数y=f（t）的大致图象如图，那么平面图形的形状不可能是（ ）
