题目内容
长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为________.
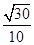
试题分析:由题知,连接
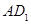 ,
,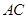 ,
,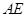 ,
,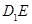 ,
,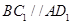 ,异面直线BC1与AE所成角,即为
,异面直线BC1与AE所成角,即为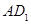 与
与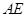 所成的角
所成的角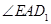 ,在
,在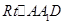 中,
中,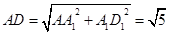 ,在
,在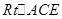 中
中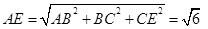 ,在
,在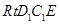 中
中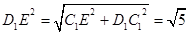 ,故由余弦定理,
,故由余弦定理,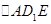 中,
中,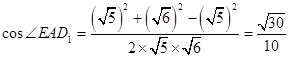 .
.
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
题目内容
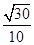
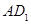 ,
,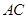 ,
,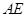 ,
,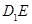 ,
,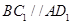 ,异面直线BC1与AE所成角,即为
,异面直线BC1与AE所成角,即为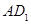 与
与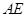 所成的角
所成的角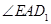 ,在
,在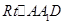 中,
中,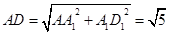 ,在
,在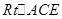 中
中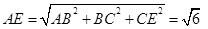 ,在
,在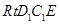 中
中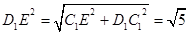 ,故由余弦定理,
,故由余弦定理,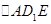 中,
中,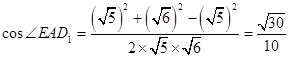 .
.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案