题目内容
20.若一个三角形的三边是连续的三个自然数,且三角形最大内角是最小内角的2倍,求此三角形三边的长.分析 设三角形三边是连续的三个自然n-1,n,n+1,三个角分别为α,π-3α,2α,由正弦定理求得cosα=$\frac{n+1}{2(n-1)}$,
再由余弦定理可得 (n-1)2=(n+1)2+n2-2(n+1)n•$\frac{n+1}{2(n-1)}$,求得n=5,从而得出结论.
解答 解:设三边长分别为n-1,n,n+1,对应的角为A,B,C,
由题意知C=2A,
由正弦定理得$\frac{n-1}{sinA}$=$\frac{n+1}{sinC}$=$\frac{n+1}{2sinAcosA}$
即有cosA=$\frac{n+1}{2(n-1)}$,
又cosA=$\frac{{n}^{2}+(n+1)^{2}-(n-1)^{2}}{2n(n+1)}$=$\frac{n+4}{2(n+1)}$
所以$\frac{n+1}{2(n-1)}$=$\frac{n+4}{2(n+1)}$,
化简为n2-5n=0,解得n=5,
所以三边分别为4,5,6.
点评 本题考查正弦定理、余弦定理的应用,求得n2-5n=0,是解题的难点,属于中档题.

练习册系列答案
相关题目
8.已知等比数列{an}前n项和为Sn,则“a1>0”是“S2013>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.将四名青年志愿者安排到三个社区参加劳动,要求每个社区至少安排一名,则不同的安排方法种数是( )
| A. | 72 | B. | 36 | C. | 24 | D. | 12 |
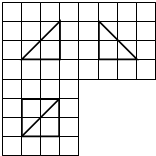 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.