题目内容
9．
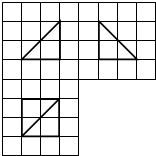如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体外接球的表面积为12π．
分析 根据三视图可知该几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，把四棱锥补成边长为2的正方体，利用正方体的对角线为外接球的直径求外接球的半径，代入球的表面积公式计算．
解答 
解：由三视图知：几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，
把四棱锥补成正方体，则正方体的边长为2，
∴正方体的外接球就是四棱锥的外接球，
∴外接球的直径2R=$\sqrt{3{×2}^{2}}$=2$\sqrt{3}$，∴R=$\sqrt{3}$，
∴外接球的表面积S=4πR2=4π×3=12π．
故答案为：12π．
点评 本题考查了由三视图求几何体的外接球的表面积，判断几何体的几何特征，是解决本题的关键．
练习册系列答案
相关题目
19．为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果．共选100名学生随机分成两个班，每班50名学生，其中一班采取“传统式教学法”，二班实行“三步式教学法”
（Ⅰ）若全校共有学生2000名，其中男生1100名，现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查，应抽取多少名女生？
（Ⅱ）下表1，2分别为实行“传统式教学”与“三步式教学”后的数学成绩：
表1
表2
完成下面2×2列联表，并回答是否有99%的把握认为这两种教学法有差异．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
参考数据：
（Ⅰ）若全校共有学生2000名，其中男生1100名，现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查，应抽取多少名女生？
（Ⅱ）下表1，2分别为实行“传统式教学”与“三步式教学”后的数学成绩：
表1
| 数学成绩 | 90分以下 | 90-120分 | 120-140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90-120分 | 120-140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下（人数） | 120分以上（人数） | 合计（人数） |
| 一班 | 35 | 15 | 50 |
| 二班 | 45 | 5 | 50 |
| 合计 | 80 | 20 | 100 |
参考数据：
| P（K2≥k0） | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |