题目内容
【题目】已知![]() 称为
称为![]() ,
,![]() 的二维平方平均数,
的二维平方平均数,![]() 称为
称为![]() ,
,![]() 的二维算术平均数,
的二维算术平均数,![]() 称为
称为![]() ,
,![]() 的二维几何平均数,
的二维几何平均数,![]() 称为
称为![]() ,
,![]() 的二维调和平均数,其中
的二维调和平均数,其中![]() ,
,![]() 均为正数.
均为正数.
(1)试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(2)令![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(3)令![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 、
、![]() 三者之间的大小关系,并证明你的猜想.
三者之间的大小关系,并证明你的猜想.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)用分析法结合基本不等式即可证得![]() .(2) 用分析法结合基本不等式即可证得
.(2) 用分析法结合基本不等式即可证得![]() .(3)先证
.(3)先证![]() 再证
再证![]() ,均采用分析法结合基本不等式进行证明.
,均采用分析法结合基本不等式进行证明.
试题解析:解:(Ⅰ)![]() ,采用分析法。欲证
,采用分析法。欲证![]() ,即证
,即证![]() ,即证
,即证![]() ,即证
,即证![]() ,上式显然成立。
,上式显然成立。
(Ⅱ)![]() 。欲证
。欲证![]() ,即证
,即证![]() ,由均值不等式可得:
,由均值不等式可得:
![]() ,等号成立的条件是
,等号成立的条件是![]() ,所以原命题成立.
,所以原命题成立.
(Ⅲ)![]() 。首先证明
。首先证明![]() :欲证
:欲证![]() ,即证
,即证![]() ,即证
,即证![]() ,即证
,即证![]() ,即证
,即证![]() ,即证
,即证![]() ,上式显然成立,等号成立的条件是
,上式显然成立,等号成立的条件是![]() ,故
,故![]() .
.
再证![]() :欲证
:欲证![]() ,即证
,即证![]() ,即证
,即证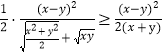 ,当
,当![]() 时,上式显然成立,当
时,上式显然成立,当![]() 时,即证
时,即证![]() ,而此式子在证明
,而此式子在证明![]() 已经成功证明,所以原命题成立。
已经成功证明,所以原命题成立。

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?

