题目内容
【题目】以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2α﹣4cosα=0．已知直线l的参数方程为
（
为参数），点M的直角坐标为
.
（1）求直线l和曲线C的普通方程；
（2）设直线l与曲线C交于A，B两点，求
.
【答案】(1)直线l的直角坐标方程为
，曲线C的直角坐标方程为y2=4x；(2)8.
【解析】【试题分析】（1）对曲线
极坐标方程两边乘以
，化简为普通方程，对直线
的参数方程，利用加减消元法消去
，化为普通方程.（2）写出直线
参数方程的标准形式，并代入曲线
的普通方程，利用直线参数的几何意义和韦达定理，求得
的值.
【试题解析】
（1）∵ρsin2α﹣2cosα=0，∴ρ2sin2α=4ρcosα，
∴曲线C的直角坐标方程为y2=4x．
由
消去
，得
.
∴直线l的直角坐标方程为
．
（2）点M（1，0）在直线l上，
设直线l的参数方程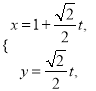
（t为参数），A，B对应的参数为t1，t2．
将l的参数方程代入y2=4x，得
.
于是
， 
.
∴
.
练习册系列答案
相关题目
【题目】某海滨浴场一天的海浪高度
是时间
的函数，记作
，下表是某天各时的浪高数据：
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
（1）选用一个三角函数来近似描述这个海滨浴场的海浪高度与时间
的函数关系；
（2）依据规定，当海浪高度不少于
时才对冲浪爱好者开放海滨浴场，请依据（1）的结论，判断一天内的
至
之间，有多少时间可供冲浪爱好者进行冲浪？
