Question

【题目】某海滨浴场一天的海浪高度是时间的函数，记作，下表是某天各时的浪高数据：

	0	3	6	9	12	15	18	21	24
	1.5	1.0	0.5	1.0	1.5	1.0	0.5	0.99	1.5

（1）选用一个三角函数来近似描述这个海滨浴场的海浪高度与时间的函数关系；

（2）依据规定，当海浪高度不少于时才对冲浪爱好者开放海滨浴场，请依据（1）的结论，判断一天内的至之间，有多少时间可供冲浪爱好者进行冲浪？

Answer 1

【答案】（1）； （2）至．

【解析】

（1）首先画出散点图，根据散点图的形式可设，根据图象的最高点和最低点可知 ，求，再根据半周期求，最后代入函数取得最大值，代入求；

（2）根据，可求的取值范围.

（1）以时间为横坐标，海浪高度为纵坐标，在平面直角坐标系中画出散点图，如图所示：

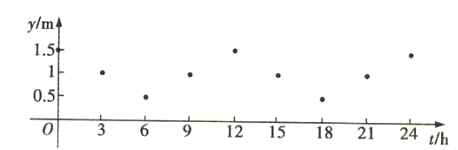
依据散点图，可以选用函数来近似描述这个海滨浴场的海浪高度与时间的函数关系.从表中数据和散点图，可知，，

所以，得.

又，于是.

由图，知，，

又，所以，从而，即.

（2）由题意，可知，所以，即，

所以，即.

又，所以或或.

故一天内的至之间有可供冲浪爱好者进行冲浪，即至.