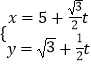题目内容
【题目】已知函数![]() 且
且![]() ).
).
(1)求![]() 的定义域;
的定义域;
(2)讨论函数![]() 的单调性.
的单调性.
【答案】(1)当![]() 时, 定义域是
时, 定义域是![]() ;当
;当![]() 时,定义域是
时,定义域是![]() ;(2)当
;(2)当![]() 时,
时,![]() 在(0,+∞)上是增函数,当
在(0,+∞)上是增函数,当![]() 时,
时,![]() 在(-∞,0)上也是增函数.
在(-∞,0)上也是增函数.
【解析】试题分析:(1)要使函数![]() 有意义,则有
有意义,则有![]() ,讨论两种情况,分别根据指数函数的性质求解不等式即可;(2)当
,讨论两种情况,分别根据指数函数的性质求解不等式即可;(2)当![]() 时,
时,![]() 是增函数,
是增函数,![]() 是增函数;当
是增函数;当![]() 时,.
时,.![]() 是减函数,
是减函数,![]() 是减函数,进而可得函数
是减函数,进而可得函数![]() 的单调性.
的单调性.
试题解析:(1)令![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() 的解集是(0,+∞);
的解集是(0,+∞);
当![]() 时,
时,![]() 的解集是(-∞,0);
的解集是(-∞,0);
所以,当![]() 时,
时,![]() 的定义域是(0,+∞);
的定义域是(0,+∞);
当![]() 时,
时,![]() 的定义域是(-∞,0).
的定义域是(-∞,0).
(2)当![]() 时,
时,![]() 是增函数,
是增函数,![]() 是增函数,从而函数
是增函数,从而函数![]() 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
同理可证:当![]() 时,函数
时,函数![]() 在(-∞,0)上也是增函数.
在(-∞,0)上也是增函数.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目