题目内容
9.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,过点M$(2,\sqrt{6})$(Ⅰ)求双曲线C的方程;
(Ⅱ)对称轴为x轴的标准抛物线w过M点,是否存在斜率为1的直线L与此抛物线W有公共点,且M点到此直线L 的距离为$\sqrt{2}$?
分析 (Ⅰ)利用双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,过点M$(2,\sqrt{6})$,建立方程,求出a,b,即可求双曲线C的方程;
(Ⅱ)求出对称轴为x轴的标准抛物线的方程,设斜率为1的直线L与此抛物线W有公共点,利用M点到此直线L 的距离为$\sqrt{2}$,即可得出结论.
解答 解:(Ⅰ)∵双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,过点M$(2,\sqrt{6})$,
∴$\frac{c}{a}$=$\sqrt{3}$,$\frac{4}{{a}^{2}}-\frac{6}{{b}^{2}}=1$,
∴a=1,b=$\sqrt{2}$,
∴双曲线C的方程为${x}^{2}-\frac{{y}^{2}}{2}=1$;
(Ⅱ)设抛物线方程为y2=ax,代入M,可得6=2a,
∴a=3,
∴抛物线方程为y2=3x,
设斜率为1的直线L的方程为y=x+m,即x-y+m=0,
∵M点到此直线L的距离为$\sqrt{2}$,
∴$\frac{|2-\sqrt{6}+m|}{\sqrt{2}}$=$\sqrt{2}$,
∴m=$\sqrt{6}$或-4+$\sqrt{6}$,
∴直线L的方程为x-y+$\sqrt{6}$=0或x-y-4+$\sqrt{6}$=0.
经检验x-y-4+$\sqrt{6}$=0,符合题意.
点评 本题考查双曲线的方程与性质,考查抛物线的方程,考查直线与抛物线的位置关系,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,0),$\overrightarrow{c}$=(3,4),若($\overrightarrow{a}$+$λ\overrightarrow{b}$)∥$\overrightarrow{c}$,λ∈R,则λ=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | 2 |
14.已知随机变量ξ服从正态分布N(2,1),且P(1≤x≤3)=a,则P(x>3)=( )
| A. | $\frac{a}{2}$ | B. | 1-$\frac{a}{2}$ | C. | 1-a | D. | $\frac{1-a}{2}$ |
18.下列图形中不能作为函数图象的是( )
| A. | 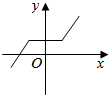 | B. | 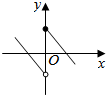 | C. |  | D. | 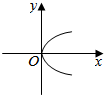 |