题目内容
19．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1，0），$\overrightarrow{c}$=（3，4），若（$\overrightarrow{a}$+$λ\overrightarrow{b}$）∥$\overrightarrow{c}$，λ∈R，则λ=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | 1 | D． | 2 |
分析 利用向量的坐标运算和向量共线定理即可得出．
解答 解：∵向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1，0），$\overrightarrow{c}$=（3，4），
∴$\overrightarrow{a}$+$λ\overrightarrow{b}$=（1+λ，2），
∵（$\overrightarrow{a}$+$λ\overrightarrow{b}$）∥$\overrightarrow{c}$，
∴4（1+λ）=2×3，
解得λ=$\frac{1}{2}$，
故选：A．
点评 本题考查了向量的坐标运算和向量共线定理，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
17．
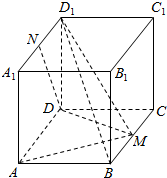已知ABCD-A1B1C1D1是长方体，且AB=AA1=2，AD=4，M是BC中点，N是A1D1中点．
（Ⅰ）求证：AM⊥平面MDD1；
（Ⅱ）求证：DN⊥MD1；
（Ⅲ）求三棱锥A-MBD1的体积．
已知ABCD-A1B1C1D1是长方体，且AB=AA1=2，AD=4，M是BC中点，N是A1D1中点．（Ⅰ）求证：AM⊥平面MDD1；
（Ⅱ）求证：DN⊥MD1；
（Ⅲ）求三棱锥A-MBD1的体积．
11．设a＞2b＞0，则（a-b）2+$\frac{9}{b（a-2b）}$的最小值是（ ）
| A． | 12 | B． | 9 | C． | 6 | D． | 3 |
8．下列命题中，真命题是（ ）
| A． | ?x0∈R，ex0≤0 | B． | a＞1，b＞1是ab＞1的充分条件 | ||
| C． | ?x∈R，2x＞x2 | D． | a+b=0的充要条件是$\frac{a}{b}$=-1 |