题目内容
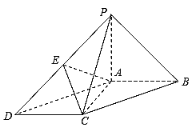
【题目】如图，在底面为平行四边形的四棱锥
中，
，
平面ABCD，且
，点E是PD的中点．
求证：
；
求证：
平面AEC．
【答案】见解析
【解析】
试题（Ⅰ）由已知得AC⊥AB，AC⊥PA，从而AC⊥平面PAB，由此能证明AC⊥PB．
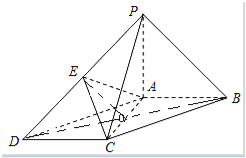
（Ⅱ）连接BD，与AC相交于O，连接EO，由已知得EO∥PB，由此能证明PB∥平面AEC．
（Ⅰ）证明：∵在底面为平行四边形的四棱锥P﹣ABCD中，
AB⊥AC，PA⊥平面ABCD，
∴AC⊥AB，AC⊥PA，
又AB∩PA=A，∴AC⊥平面PAB，
∵PB平面PAB，∴AC⊥PB．
（Ⅱ）证明：连接BD，与AC相交于O，连接EO，
∵ABCD是平行四边形，
∴O是BD的中点，又E是PD的中点，
∴EO∥PB，
又PB不包含于平面AEC，EO平面AEC，
∴PB∥平面AEC．
练习册系列答案
优生乐园系列答案
相关题目
