题目内容
【题目】函数f(x)= ![]() ,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论 ①m∈[3,4)
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论 ①m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈ ![]()
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
A.①②③
B.①②④
C.①③④
D.②③④
【答案】A
【解析】解:∵f(x)= ![]() ,∴函数f(x)的图象如下
,∴函数f(x)的图象如下 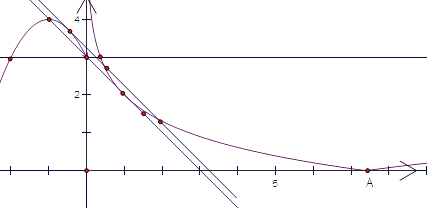
若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①正确
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b是x2+2x+m﹣3=0
的两根,∴a+b=﹣2,ab=m﹣3,∴ab∈[0,1),且lnc=2﹣m,lnd=2+m,∴ln(cd)=4∴cd=e4 ,
∴abcd∈[0,e4),∴②是正确的.
由2﹣lnx=4得x= ![]() ,由2﹣lnx=3得x=
,由2﹣lnx=3得x= ![]() ,∴c∈(
,∴c∈( ![]() ,
, ![]() ],又∵cd=e4 ,
],又∵cd=e4 ,
∴a+b+c+d=c+ ![]() ﹣2在(
﹣2在( ![]() ,
, ![]() ]是递减函数,∴a+b+c+d∈[e5+
]是递减函数,∴a+b+c+d∈[e5+ ![]() ﹣2,e6+
﹣2,e6+ ![]() ﹣2);
﹣2);
∴③是正确的
若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=﹣x+m有三个不同的交点,
而直线y=﹣x+3 与y=﹣x+ ![]() 均与y=f(x)有三个交点,∴m不唯一.∴④是不正确的
均与y=f(x)有三个交点,∴m不唯一.∴④是不正确的
故选A
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
相关题目