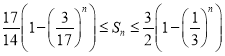题目内容

【题目】若一条直线与一个平面垂直，则称此直线与平面构成一个“正交线面对”.那么在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是（ ）

A. 48 B. 36 C. 24 D. 18

【答案】B

【解析】

两个顶点确定的直线包括：正方体的棱、面对角线、体对角线。依次寻找与上述三条直线垂直的包含四个顶点的平面，可以得到“正交线面对”的个数。

①正方体的每一条棱，都与两个侧面垂直，可得个“正交线面对”。正方体共条棱，可得“正交线面对”个

②正方体的每一条面对角线，都与一个对角面垂直，可得个“正交线面对”。正方体共条面对角线，可得“正交线面对”个

③不存在与包含正方体的四个顶点的平面与正方体的体对角线垂直

综上所述：共有个

本题正确选项：

练习册系列答案
相关题目

【题目】在直角坐标系xOy中，曲线C1： （t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2 cosθ．
（1）求C2与C3交点的直角坐标；
（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．

【题目】设函数．

（1）若函数在上为减函数，求实数的最小值；

（2）若存在，使成立，求实数的取值范围．

【题目】如图，在底面为平行四边形的四棱锥中，，平面ABCD，且，点E是PD的中点．

求证：；

求证：平面AEC．

【题目】已知各项为正的数列满足： ， （）.

（1）求；

（2）证明： （）；

（3）记数列的前项和为，求证： .

【题目】设函数 ， ，对任意， ，不等式恒成立，则正数的取值范围是__________．

【题目】设函数f（x）=﹣x3+bx（b为常数），若方程f（x）=0的根都在区间[﹣2，2]内，且函数f（x）在区间（0，1）上单调递增，则b的取值范围是（　　）
A.[3，+∞）
B.（3，4]
C.[3，4]
D.（﹣∞，4]

【题目】已知，函数.

（1）当时，解不等式；

（2）若关于的方程的解集中恰有两个元素，求的取值范围；

（3）设，若对任意，函数在区间上的最大值与最小值的和不大于，求的取值范围.

【题目】把数列的各项按顺序排列成如下的三角形状，

记表示第行的第个数，例如 = ，若=，则（ ）

A. 36 B. 37 C. 38 D. 45

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网