题目内容
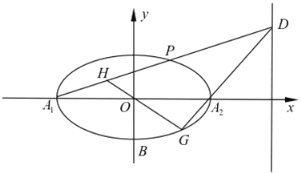
【题目】如图，在平面直角坐标系xOy中，已知椭圆C：
(a＞b＞0)的左、右顶点分别为A1(﹣2，0)，A2(2，0)，右准线方程为x＝4．过点A1的直线交椭圆C于x轴上方的点P，交椭圆C的右准线于点D．直线A2D与椭圆C的另一交点为G，直线OG与直线A1D交于点H．
（1）求椭圆C的标准方程；
（2）若HG⊥A1D，试求直线A1D的方程；
（3）如果
，试求
的取值范围．
【答案】（1）
；（2）
；（3）
【解析】
（1）由题可得：
，利用椭圆准线方程可得
，即可求得
，问题得解。
（2）设
，即可表示直线
的方程为：
，联立直线与椭圆方程可求得
，即可求得
，由HG⊥A1D可列方程
，整理得：
，结合
即可求得
，从而求得
，问题得解。
（3）设
，
，
，
，表示出直线
的方程为：
，直线
的方程为：
，将直线方程分别与椭圆方程联立，即可求得
，
，
，联立直线
的方程与直线的方程即可求得
，即可表示出
,
，利用
列方程可得：
，即可表示出
，结合
即可求得
，问题得解。
（1）由题可得：，又椭圆右准线方程为
＝4，
所以，解得：，又
，解得：
所以椭圆C的标准方程为：.
（2）设（
）,则
且
所以直线的方程为：
联立直线的方程与准线方程
可得：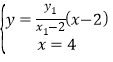
，
整理得：
，所以，
所以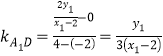
.
又HG⊥A1D，所以，即：
联立
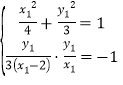可得：.
所以
.
所以直线的方程为：.
（3）设，，，，其中
直线的方程为：
联立椭圆方程可得：
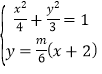，解得
直线的方程为：
联立椭圆方程可得：
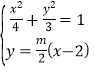，解得，
所以直线的方程为：
联立直线的方程与直线的方程可得：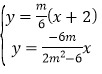
，
解得：
所以,
又，所以
所以
整理得：
因为，所以
，整理得：
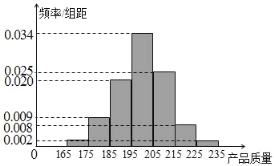
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取100件产品作为样本称出它们的质量（单位：毫克），质量值落在
的产品为合格品，否则为不合格品．如表是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图．
产品质量/毫克 | 频数 |
（165，175] | 3 |
（175，185] | 2 |
（185，195] | 21 |
（195，205] | 36 |
（205，215] | 24 |
（215，225] | 9 |
（225，235] | 5 |
（Ⅰ）根据乙流水线样本的频率分布直方图，求乙流水线样本质量的中位数（结果保留整数）；
（Ⅱ）从甲流水线样本中质量在
的产品中任取2件产品，求两件产品中恰有一件合格品的概率；
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
（Ⅲ）由以上统计数据完成下面2×2列联表，能否在犯错误的概率不超过0.15的前提下认为产品的包装合格与两条自动包装流水线的选择有关？
下面临界值表仅供参考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：
，其中n＝a+b+c+d．
