题目内容
【题目】已知过定点![]() 的动圆是
的动圆是![]() 与圆
与圆![]() 相内切.
相内切.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)设动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 是曲线
是曲线![]() 上的两点,线段
上的两点,线段![]() 的垂直平分线过点
的垂直平分线过点![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题易知,![]() 可得
可得![]() 为定值,利用椭圆的定义求得结果;
为定值,利用椭圆的定义求得结果;
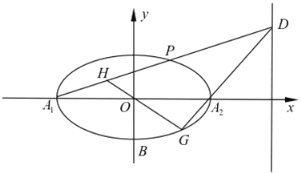
(2)设![]() 所在直线方程为
所在直线方程为![]() 椭圆联立,表示出AB的长度和
椭圆联立,表示出AB的长度和![]() 到直线
到直线![]() 的距离
的距离![]() ,求得
,求得![]() 的面积
的面积![]() ,再由题
,再由题![]() k与b的关系,可得答案.
k与b的关系,可得答案.
解:(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
设圆![]() 的半径为
的半径为![]() ,由题意知点
,由题意知点![]() 在圆
在圆![]() 内.
内.
可得![]()
所以点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
得![]()
所以动圆圆心![]() 的轨迹方程为
的轨迹方程为![]()
(2)显然![]() 不与
不与![]() 轴垂直,设
轴垂直,设![]() 所在直线方程为
所在直线方程为![]() 可得
可得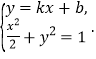
可得![]() ……①设
……①设![]() ,
,
则![]() 是方程①的两不相等的实根,得
是方程①的两不相等的实根,得
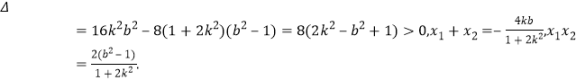
得![]()
![]()
又点![]() 到直线
到直线![]() 的距离
的距离![]()
所以![]() 的面积
的面积![]()
由题意知, ![]()
得![]()
又![]()
代入上式得![]()
得![]()
(也可直接用垂直平分线过点![]() 得到
得到![]() 关系)
关系)
当![]() 时,
时, ![]()
当![]()
![]() 有最大值
有最大值![]()
当![]() 时,
时,
![]()
当![]() 时,
时,![]() 有最大值
有最大值![]()
所以![]() 面积的最大值为
面积的最大值为![]()

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目