题目内容
18.已知函数f(x)=$\frac{mx+n}{{x}^{2}+1}$是定义在(-1,l)上的奇函数,且f(-$\frac{1}{2}$)=-$\frac{2}{5}$.(I)确定函数f(x)的解析式;
(Ⅱ)当x∈(-l,1)时,判断函数f(x)的单调性,并证明.
分析 (I)利用f(0)=0,求出n,利用f(-$\frac{1}{2}$)=-$\frac{2}{5}$,求出m,即可确定函数f(x)的解析式;
(Ⅱ)利用导数判断函数f(x)的单调性.
解答 解:(I)∵函数f(x)=$\frac{mx+n}{{x}^{2}+1}$是定义在(-1,l)上的奇函数,
∴f(0)=0,
∴n=0,
∴f(x)=$\frac{mx}{{x}^{2}+1}$,
∵f(-$\frac{1}{2}$)=-$\frac{2}{5}$,
∴m=1,
∴f(x)=$\frac{x}{{x}^{2}+1}$;
(Ⅱ)∵f(x)=$\frac{x}{{x}^{2}+1}$,
∴f′(x)=$\frac{{x}^{2}+1-x•2x}{({x}^{2}+1)^{2}}$=$\frac{-(x+1)(x-1)}{({x}^{2}+1)^{2}}$,
∵x∈(-l,1),
∴f′(x)>0,
∴当x∈(-l,1)时,函数f(x)单调递增.
点评 本题考查函数解析式的确定,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.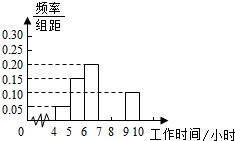 某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
(1)求表中a,b,x的值,并补齐频率分布直方图;
(2)现从工作时间在[4,5]和[6,7)内的工人中随机抽取2名,求抽到的2名工人的工作时间都在[6,7)内的概率.
 某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.| 工作时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) | [9,10) |
| 频数 | 1 | 3 | 4 | a | b | 2 |
| 频率 | 0.05 | 0.15 | 0.20 | 0.30 | x | 0.10 |
(2)现从工作时间在[4,5]和[6,7)内的工人中随机抽取2名,求抽到的2名工人的工作时间都在[6,7)内的概率.
7.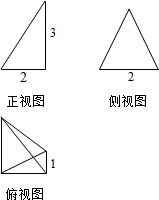 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )
 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |