题目内容
10.当-1≤a≤1时,不等式ax2+7x-1>2x+5恒成立,则x的取值范围是(2,3).分析 由题意可得不等式ax2+5x-6>0对-1≤a≤1恒成立,令f(a)=ax2+5x-6,则f(-1)>0且f(1)>0,由二次不等式的解法,即可得到所求范围.
解答 解:不等式ax2+7x-1>2x+5恒成立,即为
不等式ax2+5x-6>0对-1≤a≤1恒成立,
令f(a)=ax2+5x-6,
则f(-1)>0且f(1)>0,
即为-x2+5x-6>0且x2+5x-6>0,
即有2<x<3且x>1或x<-6.
则2<x<3.
故答案为:(2,3).
点评 本题考查函数恒成立问题的解法,考查二次不等式的解法,考查运算能力,属于中档题.

练习册系列答案
相关题目
20.钝角三角形ABC的面积为3$\sqrt{3}$,BC=3,AC=4,则AB=( )
| A. | $\sqrt{13}$ | B. | $\sqrt{37}$ | C. | 6 | D. | 7 |
19.如表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是$\stackrel{∧}{y}$=-0.7x+a,则据此模型预测6月份用水量为1.05百吨.
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
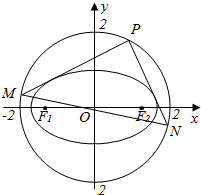 已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,离心率为$\frac{\sqrt{6}}{3}$,△ABF2的周长等于4$\sqrt{3}$,点A、B在椭圆C上,且F1在边AB上.
已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,离心率为$\frac{\sqrt{6}}{3}$,△ABF2的周长等于4$\sqrt{3}$,点A、B在椭圆C上,且F1在边AB上.