题目内容
7.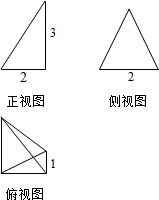 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 判断襟怀坦荡形状,通过三视图的数据,求解几何体的体积即可.
解答 解:由题意可知几何体的四棱锥,底面是直角梯形下底为2,高为2,上底为1,一个侧面与底面垂直,高为3;
如图: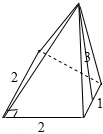
该几何体的体积为:$\frac{1}{3}×\frac{1}{2}(1+2)×2×3$=3.
故选:C.
点评 本题考查简单几何体的三视图的应用,几何体的体积的求法,判断几何体的形状是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.如表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是$\stackrel{∧}{y}$=-0.7x+a,则据此模型预测6月份用水量为1.05百吨.
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
16.下列说法正确的是( )
| A. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| B. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8 | |
| C. | “x<0”是“ln(x+1)<0”的充要条件 | |
| D. | “?x≥2,x2-3x+2≥0”的否定是“?x0<2,x02-3x0+2<0” |
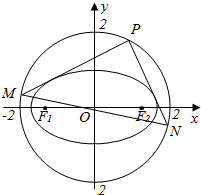 已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,离心率为$\frac{\sqrt{6}}{3}$,△ABF2的周长等于4$\sqrt{3}$,点A、B在椭圆C上,且F1在边AB上.
已知椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,离心率为$\frac{\sqrt{6}}{3}$,△ABF2的周长等于4$\sqrt{3}$,点A、B在椭圆C上,且F1在边AB上.