如果方程ax2+bx+b=0中.a＜0时.它的两根x1.x2满足x1＜x2.那么不等式ax2+bx+b＜0的解是(-∞.x1)∪(x2.+∞)．题目和参考答案——青夏教育精英家教网—

题目内容

3．如果方程ax²+bx+b=0中，a＜0时，它的两根x₁，x₂满足x₁＜x₂，那么不等式ax²+bx+b＜0的解是（-∞，x₁）∪（x₂，+∞）．

分析由方程ax²+bx+b=0的两根x₁，x₂满足x₁＜x₂，a＜0时，结合二次函数的图象和性质，可得不等式ax²+bx+b＜0的解．

解答解：∵方程ax²+bx+b=0的两根x₁，x₂满足x₁＜x₂，且a＜0，
故函数y=ax²+bx+b的图象是开口朝下的抛物线，
若ax²+bx+b＜0，则函数图象位于x轴下方，
则x＜x₁，或x＞x₂，
即不等式ax²+bx+b＜0的解是（-∞，x₁）∪（x₂，+∞），
故答案为：（-∞，x₁）∪（x₂，+∞）

点评本题考查了一元二次不等式的知识，有一定的难度，本题的技巧性较强，在解答此类题目时要注意与一元二次方程的结合．

练习册系列答案

14．已知，命题p：已知m≠0，若2^a＞2^b，则am²＞bm²，则其否命题为（　　）

	A．	已知m=0，若2^a＞2^b，则am²＞bm²		B．	已知m≠0，若2^a≤2^b，则am²＞bm²
	C．	已知m≠0，若2^a＞2^b，则am²≤bm²		D．	已知m≠0，若2^a≤2^b，则am²≤bm²

11．从6所学校选出9名学生组成代表团，每校至少有一人的选法有多少种？

18．已知函数f（x）=$\frac{mx+n}{{x}^{2}+1}$是定义在（-1，l）上的奇函数，且f（-$\frac{1}{2}$）=-$\frac{2}{5}$．
（I）确定函数f（x）的解析式；
（Ⅱ）当x∈（-l，1）时，判断函数f（x）的单调性，并证明．

8．解不等式：|x+1|≥|2x-1|

15．

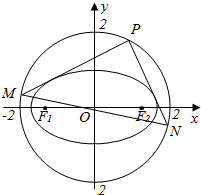已知椭圆：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点为F₁，F₂，离心率为$\frac{\sqrt{6}}{3}$，△ABF₂的周长等于4$\sqrt{3}$，点A、B在椭圆C上，且F₁在边AB上．
（1）求椭圆C的标准方程；
（2）如图，过圆O：x²+y²=4上任意一点P作椭圆C的两条切线PM和PN与圆O交于点M、N，求△PMN面积的最大值．

12．化简：
（1）mtan0°+xcos90°-psin180°-qcos270°-rsin360°；
（2）sin（-1320°）cos1110°+cos（-1020°）sin750°+tan390°．

13．函数y=2-$\sqrt{4x-{x}^{2}}$（x∈[0，4]）的值域是（　　）

[-$\sqrt{2}$，$\sqrt{2}$]

试题分类