题目内容

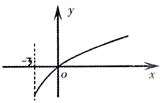
已知函数f（x）的定义域为[-3，+∞），且f（6）=f（-3）=2．f′（x）为f（x）的导函数，f′（x）的图象如图所示．若正数a，b满足f（2a+b）＜2，则
b+3
a-2
的取值范围是（　　）
A．（-
3
2
，3）		B．（-∞，-
3
2
）∪（3，+∞）
C．（-
9
2
，3）		D．（-∞，-
9
2
）∪（3，+∞）

如图所示：f′（x）≥0在[-3，+∞）上恒成立
∴函数f（x）在[-3，0）是减函数，（0，+∞）上是增函数，
又∵f（2a+b）＜2=f（6）
∴
2a+b＞0
2a+b＜6

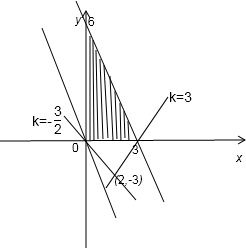
画出平面区域
令t=
b+3
a-2
表示过定点（2，-3）的直线的斜率
如图所示：t∈（-∞，-
3
2
）∪（3，+∞）
故选B
练习册系列答案
相关题目
某商店七月份营销一种饮料的销售利润y（万元）与销售量x（万瓶）之间函数关系的图象如图1中折线所示，该商店截止到13日调价时的销售利润为4万元，截止至15日进货时的销售利润为5.5万元．（销售利润=（售价-成本价）×销售量）
请你根据图象及商店七月份该饮料的所有销售记录提供的信息（图2），解答下列问题：
（1）求销售量x为多少时，销售利润为4万元；
（2）分别求出线段AB与BC所对应的函数关系式；
（3）我们把销售每瓶饮料所获得的利润称为利润率，那么，在OA、AB、BC三段所表示的销售信息中，哪一段的利润率最大？（直接写出答案）
已知函数f（x）=a+
1
4x+1
满足f（-x）+f（x）=0，则a的值为（　　）
A．1B．
1
4
C．-
1
2
D．-1
若a，b，c，d是正数，且满足a+b+c+d=4，用M表示a+b+c，a+b+d，a+c+d，b+c+d中的最大者，则M的最小值为______．
在下列函数中，最小值不是2的是（　　）
A．y=|x|+
1
|x|
B．y=
x2+2
x2+1
C．y=lgx+logx10D．y=3x+3-x
函数y=
1
2x+1
的值域是（　　）
A．（0，1）B．（0，1]C．（-∞，1]D．[0，1]
若函数f（3x+2）=3x+x+2，则f（3）的值是（　　）
A．3B．6C．17D．32
已知函数f（x）=sinx，对于满足0＜x1＜x2＜π的任意x1，x2，给出下列结论：
①（x2-x1）[f（x2）-f（x1）]＞0；②x2f（x1）＞x1f（x2）；③f（x2）-f（x1）＜x2-x1；④
f(x1)+f(x2)
2
＜f(
x1+x2
2
)，
其中正确结论的个数为______．
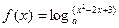如果函数的最大值为-1，那么实数         

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网