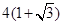题目内容
如图，三棱柱ABC—A1B1C1的侧面AA1B1B为正方形，侧面BB1C1C为菱形，∠CBB1＝60°，AB⊥B1C.
(1)求证：平面AA1B1B⊥平面BB1C1C；
(2)若AB＝2，求三棱柱ABC—A1B1C1的体积．
(1)求证：平面AA1B1B⊥平面BB1C1C；
(2)若AB＝2，求三棱柱ABC—A1B1C1的体积．
（1）见解析 （2）2
(1)由侧面AA1B1B为正方形，知AB⊥BB1.
又AB⊥B1C，BB1∩B1C＝B1，所以AB⊥平面BB1C1C，
又AB?平面AA1B1B，所以平面AA1B1B⊥平面BB1C1C.
(2)由题意，CB＝CB1，设O是BB1的中点，连接CO，则CO⊥BB1.
由(1)知，CO⊥平面AA1B1B，且CO＝
BC＝AB＝.
连结AB1，则VC—ABB1＝
S△ABB1·CO＝
AB2·CO＝
.
因为VB1—ABC＝VC—ABB1＝VABC—A1B1C1＝，
故三棱柱ABC—A1B1C1的体积VABC—A1B1C1＝2.
又AB⊥B1C，BB1∩B1C＝B1，所以AB⊥平面BB1C1C，
又AB?平面AA1B1B，所以平面AA1B1B⊥平面BB1C1C.
(2)由题意，CB＝CB1，设O是BB1的中点，连接CO，则CO⊥BB1.
由(1)知，CO⊥平面AA1B1B，且CO＝
BC＝AB＝.连结AB1，则VC—ABB1＝
S△ABB1·CO＝AB2·CO＝.因为VB1—ABC＝VC—ABB1＝
VABC—A1B1C1＝，故三棱柱ABC—A1B1C1的体积VABC—A1B1C1＝2
.
练习册系列答案
相关题目
的四棱锥S﹣ABCD的底面是边长为1的正方形，点S，A，B，C，D均在半径为1的同一球面上，则底面ABCD的中心与顶点S之间的距离为（ ）
