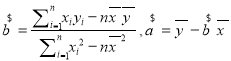题目内容
【题目】在古代,直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.三国时期吴国数学家赵爽用“弦图”( 如图) 证明了勾股定理,证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实.”这里的“实”可以理解为面积.这个证明过程体现的是这样一个等量关系:“两条直角边的乘积是两个全等直角三角形的面积的和(朱实二 ),4个全等的直角三角形的面积的和(朱实四) 加上中间小正方形的面积(黄实) 等于大正方形的面积(弦实)”. 若弦图中“弦实”为16,“朱实一”为![]() ,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )
,现随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵弦图中“弦实”为16,“朱实一”为![]()
∴大正方形的面积为16,一个直角三角形的面积为![]()
设“勾”为![]() ,“股”为
,“股”为![]() ,则
,则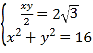 ,解得
,解得![]() 或
或![]() .
.
∵![]()
∴![]() ,即
,即![]() .
.
∴![]()
∴小正方形的边长为![]()
∴随机向弦图内投入一粒黄豆(大小忽略不计),则其落入小正方形内的概率为![]() .
.
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目