题目内容
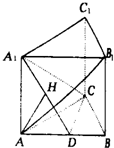
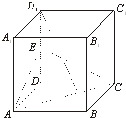
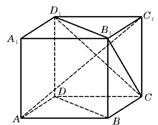
在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
(1)求证:CF∥平面A1DE;
(2)求点A到平面A1DE的距离.
(1)求证:CF∥平面A1DE;
(2)求点A到平面A1DE的距离.

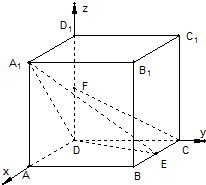
解 分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角
坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),则
=(2,0,2),
=(1,2,0)
设平面A1DE的法向量是
=(a,b,c)
则
,
=(-2,1,2)
(1)
=(0,-2,1),
∴
•
=-2+2=0,∴
⊥
,
所以,CF∥平面A1DE.
(2)点A到平面A1DE的距离是
d=
=
.
点A到平面A1DE的距离
.

坐标系,则A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),则
| DA1 |
| DE |
设平面A1DE的法向量是
| n |
则
|
| n |
(1)
| CF |
∴
| CF |
| n |
| CF |
| n |
所以,CF∥平面A1DE.
(2)点A到平面A1DE的距离是
d=
|
| ||||
|
|
| 4 |
| 3 |
点A到平面A1DE的距离
| 4 |
| 3 |


练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 为正方形,
为正方形,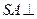 平面
平面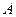 且垂直于
且垂直于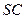 的平面分别交
的平面分别交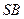 ,
,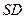 于
于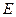 ,
,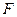 ,
,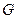 .求证:
.求证: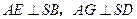 .
.