题目内容
三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=1,PB=PC=
,则点P到平面ABC的距离为( )
| 2 |
A.
| B.
| C.
| D.1 |
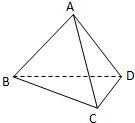
∵三棱锥P-ABC中,PA、PB、PC两两互相垂直
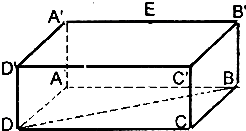
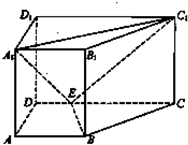
∴构造一个以PA、PB、PC为长宽高的长方体(如图)
三棱锥P-ABC的体积=
S△ABC×d(d为点P到平面ABC的距离)
三棱锥C-ABP的体积=
S△ABP×PC,
∵三棱锥P-ABC的体积=三棱锥C-ABP的体积,
∴
S△ABC×d=
S△ABP×PC,
则d=
,
则点P到平面ABC的距离为
故选:A
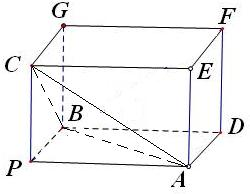
∴构造一个以PA、PB、PC为长宽高的长方体(如图)
三棱锥P-ABC的体积=
| 1 |
| 3 |
三棱锥C-ABP的体积=
| 1 |
| 3 |
∵三棱锥P-ABC的体积=三棱锥C-ABP的体积,
∴
| 1 |
| 3 |
| 1 |
| 3 |
则d=
| ||
| 2 |
则点P到平面ABC的距离为
| ||
| 2 |
故选:A


练习册系列答案
相关题目
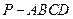 中,底面
中,底面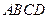 为正方形,侧面
为正方形,侧面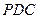 为正三角形,且平面
为正三角形,且平面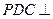 底面
底面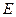 为
为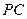 中点,求证:
中点,求证: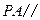 平面
平面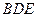 ; (2)平面
; (2)平面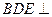 平面
平面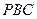 .
.
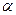 的距离依次为a、b、c,且点A与边BC在平面
的距离依次为a、b、c,且点A与边BC在平面