题目内容
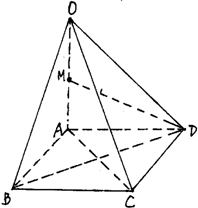
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
(1)求证:直线BD⊥平面OAC;
(2)求点A到平面OBD的距离.
(1)求证:直线BD⊥平面OAC;
(2)求点A到平面OBD的距离.

(1)证明:∵ABCD是正方形,∴BD⊥AC,
∵OA⊥底面ABCD,
BD?平面ABCD,∴OA⊥BD,AC∩OA=A,∴BD⊥平面OAC.…(5分)
(2)设点A到平面OBD的距离为h
S△ABD=
×AB×AD=
,S△OBD=
×
×
=
.
由VA-OBD=VO-ABD得
S△OBD×h=
S△ABD×OA⇒h=
所以点A到平面OBD的距离为
…(12分)
∵OA⊥底面ABCD,
BD?平面ABCD,∴OA⊥BD,AC∩OA=A,∴BD⊥平面OAC.…(5分)
(2)设点A到平面OBD的距离为h
S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 | ||
|
| 3 |
| 2 |
由VA-OBD=VO-ABD得
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
所以点A到平面OBD的距离为
| 2 |
| 3 |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 是
是 的直径,
的直径, 垂直于
垂直于 是圆周上不同于
是圆周上不同于 ,
, 的任意一点.
的任意一点.
 平面
平面 .
.