题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为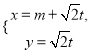 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 经过曲线
经过曲线![]() 的左焦点
的左焦点![]() .
.
(1)求![]() 的值及直线
的值及直线![]() 的普通方程;
的普通方程;
(2)设曲线![]() 的内接矩形的周长为
的内接矩形的周长为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)见解析.(2)![]() .
.
【解析】试题分析:(1)将![]() ,
, ![]() 代入上式并化简得
代入上式并化简得![]() ,所以
,所以![]() ,又直线
,又直线![]() 的普通方程为
的普通方程为![]() ,将焦点代入得得
,将焦点代入得得![]() ,所以直线
,所以直线![]() 的普通方程为
的普通方程为![]() ;(2)设椭圆
;(2)设椭圆![]() 的内接矩形在第一象限的顶点为
的内接矩形在第一象限的顶点为![]() ,所以椭圆
,所以椭圆![]() 的内接矩形的周长为
的内接矩形的周长为![]() (其中
(其中![]() ),此时椭圆
),此时椭圆![]() 的内接矩形的周长取得最大值
的内接矩形的周长取得最大值![]() .
.
试题解析:
(1)因为曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,将
,将![]() ,
, ![]() 代入上式并化简得
代入上式并化简得![]() ,所以曲线
,所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,于是
,于是![]() ,
, ![]() ,
,
直线![]() 的普通方程为
的普通方程为![]() ,将
,将![]() 代入直线方程得
代入直线方程得![]() ,所以直线
,所以直线![]() 的普通方程为
的普通方程为![]() .
.
(2)设椭圆![]() 的内接矩形在第一象限的顶点为
的内接矩形在第一象限的顶点为![]() (
(![]() ),所以椭圆
),所以椭圆![]() 的内接矩形的周长为
的内接矩形的周长为![]() (其中
(其中![]() ),此时椭圆
),此时椭圆![]() 的内接矩形的周长取得最大值
的内接矩形的周长取得最大值![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
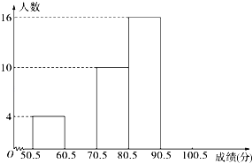
【题目】从一批草莓中,随机抽取![]() 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
分组(重量) |
|
|
|
|
频数(个) |
|
|
|
|
已知从![]() 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在![]() 的草莓的概率为
的草莓的概率为![]() .
.
(1)求出![]() ,
,![]() 的值;
的值;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的草莓中共抽取
的草莓中共抽取![]() 个,再从这
个,再从这![]() 个草莓中任取
个草莓中任取![]() 个,求重量在
个,求重量在![]() 和
和![]() 中各有
中各有![]() 个的概率.
个的概率.