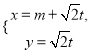[题目]设命题函数的值域为,命题.不等式恒成立.如果命题“ 为真命题.且“ 为假命题.求实数的取值范围. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设命题函数的值域为；命题，不等式恒成立，如果命题“”为真命题，且“”为假命题，求实数的取值范围。

【答案】

【解析】

试题根据若命题“P或Q”为真命题，且“P且Q”为假命题知道P和Q一真一假，分两种情况进行讨论：P真Q假和P假Q真，再根据二次函数的恒成立问题的解法和不等式的恒成立问题的解法解题，要把每种情况都讨论清楚，不要遗漏知识点.

试题解析：若命题“P或Q”为真命题，且“P且Q”为假命题，则有P和Q一真一假, .2分

先求出P,Q都为真时a的取值：

当P为真时，即对任意的，都有恒成立,

则，解得, 4分

当Q为真时，在区间上的最大值是3,

则有恒成立，解得, 6分

由上知当P,Q一真一假时有：

P真Q假P假Q真, 10分

解得. ...12分

练习册系列答案

相关题目

【题目】已知椭圆的中心在原点，焦点在轴上，短轴长和焦距都等于2，是椭圆上的一点，且在第一象限内，过且斜率等于的直线与椭圆交于另一点，点关于原点的对称点为.

（Ⅰ）证明：直线的斜率为定值；

（Ⅱ）求面积的最大值，并求此时直线的方程.

【题目】已知函数．

（1）当时，求函数的极值；

（2）设函数在处的切线方程为，若函数是上的单调增函数，求的值；

（3）是否存在一条直线与函数的图象相切于两个不同的点？并说明理由．

【题目】研究变量，得到一组样本数据，进行回归分析，有以下结论

①残差平方和越小的模型，拟合的效果越好；

②用相关指数来刻画回归效果，越小说明拟合效果越好；

③线性回归方程对应的直线至少经过其样本数据点中的一个点；

④若变量和之间的相关系数为，则变量和之间的负相关很强.

以上正确说法的个数是（）

A. B. C. D.

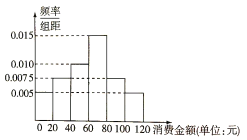
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与的人机大战中中盘弃子认输，至此柯洁与的三场比赛全部结束，柯洁三战全负，这次人机大战再次引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查，根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.