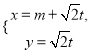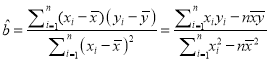题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,双曲线
,双曲线![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 的直线与抛物线在第一象限的交点为
的直线与抛物线在第一象限的交点为![]() ,且抛物线在点
,且抛物线在点![]() 处的切线与直线
处的切线与直线![]() 垂直,则
垂直,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
【答案】B
【解析】由题可知抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线方程为
的直线方程为![]() ,联立方程组
,联立方程组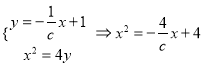
![]() ,
, ![]() ,由题可知,
,由题可知, ![]() ,
, ![]() (舍去),又由
(舍去),又由![]() ,因此
,因此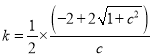
![]() ,又由题可知
,又由题可知![]() ,即得
,即得![]() ,又
,又 ![]() ,当且仅当
,当且仅当![]() 时,取等号,即
时,取等号,即![]() ,故选B.
,故选B.
【易错点晴】本题主要考查抛物线、双曲线的方程与性质、导数的几何意义以及利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用![]() 或
或![]() 时等号能否同时成立).
时等号能否同时成立).

练习册系列答案
相关题目