题目内容
1.已知函数f(x)=ln$\frac{x}{1-x}$,若f(a)+f(b)=0,且0<a<b,则ab的取值范围是(0,$\frac{1}{4}$).分析 利用函数关系式得出ln$\frac{a}{1-a}$$+ln\frac{b}{1-b}$=0,即$\frac{a}{1-a}$$•\frac{b}{1-b}$=1.a+b=1,考虑基本不等式求解即可.
解答 解:∵函数f(x)=ln$\frac{x}{1-x}$,若f(a)+f(b)=0,
∴ln$\frac{a}{1-a}$$+ln\frac{b}{1-b}$=0,
即$\frac{a}{1-a}$$•\frac{b}{1-b}$=1.
化简得出:a+b=1,又0<a<b,
利用基本不等式得出:ab$<\frac{(a+b)^{2}}{4}$=1.ab>0,
∴ab的取值范围是(0,$\frac{1}{4}$),
故答案为:(0,$\frac{1}{4}$).
点评 本题考察了对数函数的性质,基本不等式的性质,属于综合题目,但是化简难度不大.

练习册系列答案
相关题目
12.函数y=cos2(x-$\frac{π}{2}$)-sin2(x-$\frac{π}{2}$)是( )
| A. | 周期为2π的奇函数 | B. | 周期为2π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的偶函数 |
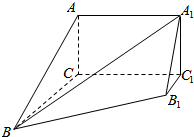 如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1
如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1