题目内容
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 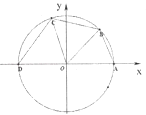
(Ⅰ)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
【答案】解:(Ⅰ)∵B( ![]() ,
, ![]() ), ∴cos∠AOB=
), ∴cos∠AOB= ![]() ,sin∠AOB=
,sin∠AOB= ![]() ;
;
∴cos∠AOC=cos(∠AOB+∠BOC)
=cos∠AOBcos∠BOC﹣sin∠AOBsin∠BOC
= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() ;
;
(Ⅱ)等腰三角形AOB中,求得|AB|=2|OB|sin ![]() =2sin
=2sin ![]() ,
,
等腰三角形COD中,求得
|CD|=2|OC|sin 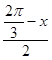 =2sin(
=2sin( ![]() ﹣
﹣ ![]() );
);
∴y=|AB|+|BC|+|CD|+|DA|
=3+2sin ![]() +2sin(
+2sin( ![]() ﹣
﹣ ![]() )
)
=3+2sin( ![]() +
+ ![]() );
);
由0<x< ![]() 得,当
得,当 ![]() +
+ ![]() =
= ![]() ,
,
即x= ![]() 时,y取得最大值5
时,y取得最大值5
【解析】(Ⅰ)由三角函数的定义,写出cos∠AOB与sin∠AOB的值,再计算cos∠AOC的值;(Ⅱ)根据等腰三角形的知识,求出|AB|、|CD|的值,再写出函数y的解析式,求出y的最大值即可.
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.

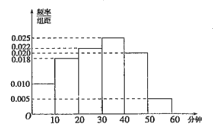
【题目】有三个游戏规则如表,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
游戏1 | 游戏2 | 游戏3 |
袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
问其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
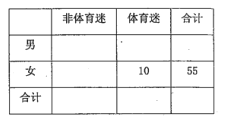
【题目】为了解某社区居民的家庭年收入与年支出的关系,相关部门随机调查了该社区5户家庭,得到如表统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
(1)根据上表可得回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
,据此估计,该社区一户年收入为15万元的家庭年支出为多少?
(2)若从这5个家庭中随机抽选2个家庭进行访谈,求抽到家庭的年收入恰好一个不超过10万元,另一个超过11万元的概率.