题目内容
【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2,则点集{P|
=2,则点集{P| ![]() =x
=x ![]() +y
+y ![]() ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
【答案】4 ![]()
【解析】解:∵| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2, 不妨设
=2, 不妨设 ![]() =(2,0),
=(2,0), ![]() =(m,n),
=(m,n),
∴ ![]() =2,2m=2,
=2,2m=2,
解得m=1,n= ![]() .
.
∵ ![]() =x
=x ![]() +y
+y ![]() ,=x(2,0)+y
,=x(2,0)+y ![]() =
= ![]() .
.
令a=2x+y,b= ![]() ,
,
解得 ![]() ,x=
,x= ![]() ,
,
由|x|+|y|≤1,x,y∈R,可得 ![]() +
+ ![]() ≤1,
≤1,
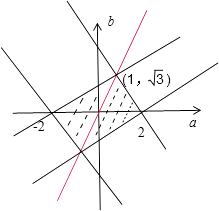
对a,b分类讨论,画出图形,可得(a,b)满足的区域为图中阴影部分.
可得(a,b)满足的区域的面积为 ![]() =4
=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】关于本题考查的平面向量的基本定理及其意义,需要了解如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某公司对新研发的一种产品进行合理定价,且销量与单价具有相关关系,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(单位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(单位:万件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)现有三条y对x的回归直线方程: ![]() =﹣10x+170;
=﹣10x+170; ![]() =﹣20x+250;
=﹣20x+250; ![]() =﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
=﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入﹣成本)