题目内容
【题目】已知函数![]()
(Ⅰ)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,求证:
,求证:![]()
.
【答案】(1)![]() 在
在![]() 上递增;(2)
上递增;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由于![]() ,导函数的零点不能直接求出,考虑二次求导,求出
,导函数的零点不能直接求出,考虑二次求导,求出![]() 的最值,从而判断出函数
的最值,从而判断出函数![]() 的单调性;(2)由题意可知当
的单调性;(2)由题意可知当![]() 时,
时,![]() ,可通过讨论研究导函数的单调性和最值,得到
,可通过讨论研究导函数的单调性和最值,得到![]() 的最小值,得到参数
的最小值,得到参数![]() 的取值范围;(3)由题意可得
的取值范围;(3)由题意可得![]() ,可考虑证明两个和为
,可考虑证明两个和为![]() 的自变量对应的函数值的积为定值
的自变量对应的函数值的积为定值![]() ,通过整理
,通过整理![]() 并放缩可实现上述设想,最终得证.
并放缩可实现上述设想,最终得证.
试题解析:(1)![]() ,令
,令![]() ,则
,则![]() ,
,
则当![]() 时,
时,![]()
![]() 单调递减,当
单调递减,当![]() 时,
时,![]()
![]() 单调递增.
单调递增.
所以有![]() ,所以
,所以![]()
(2)当![]() 时,
时,![]() ,令
,令![]() ,则
,则![]() ,则
,则![]() 单调递增,
单调递增,![]()
当![]() 即
即![]() 时,
时,![]() ,
,![]() 成立;
成立;
当![]() 时,存在
时,存在![]() ,使
,使![]() ,则
,则![]() 减,则当
减,则当![]() 时,
时,![]() ,不合题意.综上
,不合题意.综上![]()
(3)![]() ,
,
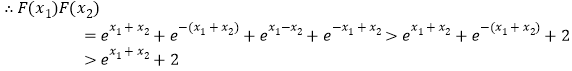
![]() ,
,
![]() ,……,
,……,![]() .
.
由此得,![]()
故![]() (
(![]() )
)

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:
甲 | 88 | 89 | 92 | 90 | 91 |
乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)