题目内容
若抛物线的顶点在原点,其准线方程过双曲线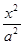 -
-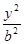 =1(
=1(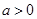 ,
,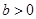 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于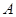 (
(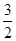 ,
,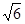 ),
),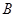 (
(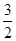 ,-
,-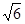 ),求两曲线的标准方程.
),求两曲线的标准方程.
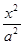 -
-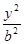 =1(
=1(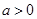 ,
,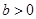 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于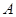 (
(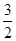 ,
,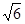 ),
),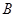 (
(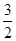 ,-
,-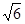 ),求两曲线的标准方程.
),求两曲线的标准方程.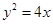 ,
,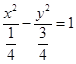 .
.根据抛物线的准线过双曲线的焦点,再根据过点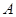 (
(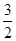 ,
,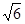 ),可得抛物线方程,由此可求出双曲线的焦点坐标,再根据双曲线的定义可得
),可得抛物线方程,由此可求出双曲线的焦点坐标,再根据双曲线的定义可得
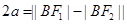 ,从而可求出双曲线的方程.
,从而可求出双曲线的方程.
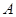 (
(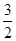 ,
,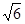 ),可得抛物线方程,由此可求出双曲线的焦点坐标,再根据双曲线的定义可得
),可得抛物线方程,由此可求出双曲线的焦点坐标,再根据双曲线的定义可得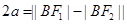 ,从而可求出双曲线的方程.
,从而可求出双曲线的方程.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
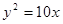 的焦点到准线的距离是
的焦点到准线的距离是 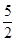
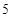
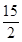
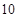
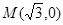 ,椭圆
,椭圆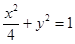 与直线
与直线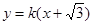 交于点
交于点 、
、 ,则
,则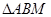 的周长为 .
的周长为 .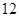 ,离心率为
,离心率为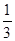 ,则椭圆的方程是( )
,则椭圆的方程是( )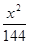 +
+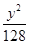 =1
=1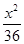 +
+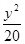 =1
=1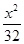 +
+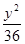 =1
=1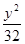 =1
=1 的周长是8,
的周长是8, ,则顶点A的轨迹方程是( )
,则顶点A的轨迹方程是( ) 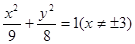
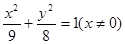
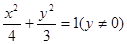
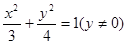
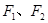 分别是双曲线
分别是双曲线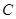 :
: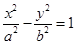 (
(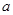 >0,
>0,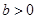 )的左、右焦点,
)的左、右焦点,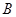 是虚轴的端点,直线
是虚轴的端点,直线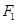
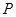 、
、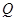 两点,线段
两点,线段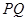 的垂直平分线与
的垂直平分线与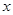 轴交于点
轴交于点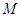 ,若
,若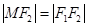 ,则
,则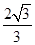
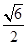
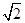
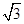
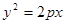 与直线
与直线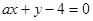 交于两点
交于两点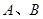 ,其中点
,其中点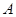 的坐标是
的坐标是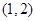 ,设抛物线的焦点为
,设抛物线的焦点为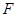 ,则
,则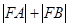 等于 ( )
等于 ( )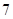
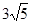
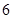
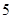
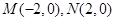 ,动点
,动点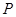 满足条件
满足条件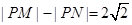 .记动点
.记动点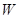 .
.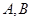 是
是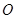 是坐标原点,求
是坐标原点,求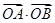 的最小值.
的最小值.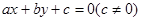 与抛物线
与抛物线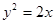 交于P、Q两点,F为抛物线的焦点,直线PF,QF分别交抛物线点M、N,则直线MN的方程为 。
交于P、Q两点,F为抛物线的焦点,直线PF,QF分别交抛物线点M、N,则直线MN的方程为 。