题目内容
16.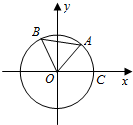 如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.
如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.(Ⅰ)求$\frac{1+sin2α}{1+cos2α}$的值;
(Ⅱ)求cos∠COB的值.
分析 (Ⅰ)由A的坐标,利用任意角的三角函数定义求出sinα与cosα的值,原式利用二倍角的正弦、余弦函数公式化简,将各自的值代入计算即可求出值;
(Ⅱ)由三角形AOB为等边三角形,得到∠AOB=60°,表示出∠COB,利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答 解:(Ⅰ)∵A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),
∴根据三角函数的定义可知,sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,
∴$\frac{1+sin2α}{1+cos2α}$=$\frac{1+2sinαcosα}{2co{s}^{2}α}$=$\frac{49}{18}$;
(Ⅱ)∵△AOB为正三角形,
∴∠AOB=60°,
∵∠COA=α,
∴cos∠COB=cos(α+60°)=cosαcos60°-sinαsin60°=$\frac{3}{5}$×$\frac{1}{2}$-$\frac{4}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{3-4\sqrt{3}}{10}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x+y-8≤0\\ x≥1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
11.若命题p:x=4,命题q:x2=16,则p是q的( )
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
8.已知函数$f(x)=sin(x-\frac{π}{2})(x∈R)$,下面结论错误的是( )
| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间$[0,\frac{π}{2}]$上单调递增 | ||
| C. | 函数f(x)的图象关于y轴对称 | D. | 点(π,0)是函数f(x)的一个对称中心 |
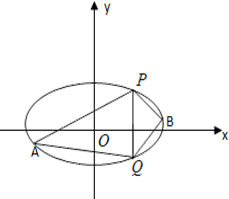 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.