题目内容
6.在锐角△ABC中,三角形内角A,B,C所对的边分别为a,b,c,设$\overrightarrow{m}$=(cosA,sinA),$\overrightarrow{n}$=(cosA,-sinA),a=$\sqrt{7}$,且$\overrightarrow{m}•\overrightarrow{n}$=-$\frac{1}{2}$(1)若b=3,求△ABC的面积;
(2)求b+c的最大值.
分析 (1)由题意和数量积运算易得A=60°,由余弦定理可得c值,代入面积公式可得;
(2)由(1)和余弦定理可得7=b2+c2-bc=(b+c)2-3bc,由基本不等式可得(b+c)2-7=3bc≤3$(\frac{b+c}{2})^{2}$,解关于b+c的不等式可得.
解答 解:(1)由题意可得$\overrightarrow{m}•\overrightarrow{n}$=cos2A-sin2A=cos2A=$-\frac{1}{2}$,
∴cos2A=-$\frac{1}{2}$,∵A为锐角,则2A=120°,解得A=60°,
由余弦定理可得a2=b2+c2-2bccosA,
代入数据可得7=9+c2-6c×$\frac{1}{2}$,
解得c=1或c=2.
当c=1时cosB=$\frac{1+7-9}{2×1×\sqrt{7}}$<0,
不满足三角形为锐角三角形,故c=2
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{3\sqrt{3}}{2}$;
(2)由(1)和余弦定理可得a2=b2+c2-2bccosA,
∴7=b2+c2-bc=(b+c)2-3bc,
∴(b+c)2-7=3bc≤3$(\frac{b+c}{2})^{2}$,
解得b+c≤2$\sqrt{7}$,当且仅当b=c=$\sqrt{7}$时取等号,
∴b+c的最大值为2$\sqrt{7}$
点评 本题考查解三角形,涉及余弦定理以及基本不等式的应用,属中档题.

练习册系列答案
相关题目
14.若二项式(x2-$\frac{2}{x}$)n展开式的第5项是常数项,则展开式的中间项为( )
| A. | -160 | B. | -160x3 | C. | 20 | D. | 160x3 |
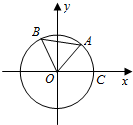 如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.
如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.