题目内容
8.已知函数$f(x)=sin(x-\frac{π}{2})(x∈R)$,下面结论错误的是( )| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间$[0,\frac{π}{2}]$上单调递增 | ||
| C. | 函数f(x)的图象关于y轴对称 | D. | 点(π,0)是函数f(x)的一个对称中心 |
分析 由条件利用诱导公式化简函数的解析式为f(x)=-cosx,再利用余弦函数的图象、性质,逐一判断各个选项是否正确,从而得出结论.
解答 解:对于函数f(x)=sin(x-$\frac{π}{2}$)=-cosx,由于它的周期为2π,故A正确;
显然,f(x)在区间$[0,\frac{π}{2}]$上单调递增,故B正确;
再根据f(x)为偶函数,它的图象关于y轴对称,可得C正确;
由于当x=π时,求得f(x)=1,故点(π,0)不会是函数f(x)的一个对称中心,故D错误,
故选:D.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
2.已知f′(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)>0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
3.已知角α的终边经过点P(0,3),则α是( )
| A. | 第一象限角 | B. | 终边在x轴的非负半轴上的角 | ||
| C. | 第四象限角 | D. | 终边在y轴的非负半轴上的角 |
20.观察式子:1+$\frac{1}{{2}^{2}}$<$\frac{3}{2}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$<$\frac{5}{3}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$<$\frac{7}{4}$,…,则可归纳出式子为( )
| A. | 1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}<\frac{1}{2n-1}$ | B. | 1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}<\frac{1}{2n+1}$ | ||
| C. | 1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}<\frac{2n-1}{n}$ | D. | 1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}<\frac{2n}{2n+1}$ |
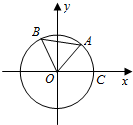 如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.
如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α.